Note
Go to the end to download the full example code
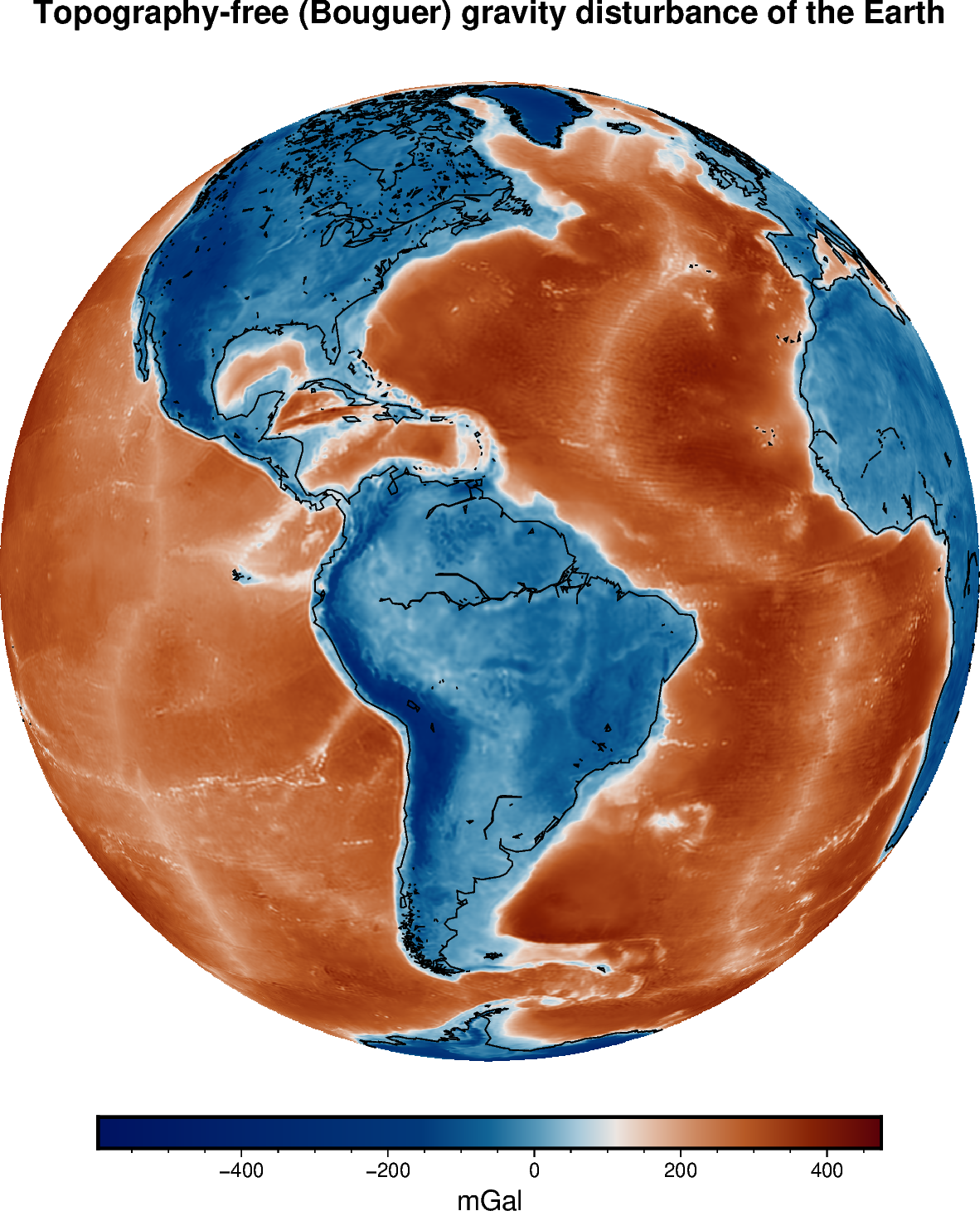
Topography-free (Bouguer) Gravity Disturbances#
The gravity disturbance is the observed gravity minus the normal gravity
(boule.Ellipsoid.normal_gravity). The signal that is left is assumed to
be due to the differences between the actual Earth and the reference ellipsoid.
Big components in this signal are the effects of topographic masses outside of
the ellipsoid and residual effects of the oceans (we removed ellipsoid crust
where there was actually ocean water). These two components are relatively well
known and can be removed from the gravity disturbance. The simplest way of
calculating the effects of topography and oceans is through the Bouguer plate
approximation.
We’ll use harmonica.bouguer_correction to calculate a topography-free
gravity disturbance for Earth using our sample gravity and topography data. One
thing to note is that the ETOPO1 topography is referenced to the geoid, not the
ellipsoid. Since we want to remove the masses between the surface of the Earth
and ellipsoid, we need to add the geoid height to the topography before Bouguer
correction.
<xarray.Dataset> Size: 65MB
Dimensions: (longitude: 2161, latitude: 1081)
Coordinates:
* longitude (longitude) float64 17kB -180.0 -179.8 -179.7 ... 179.8 180.0
* latitude (latitude) float64 9kB -90.0 -89.83 -89.67 ... 89.67 89.83 90.0
height (latitude, longitude) float32 9MB 1e+04 1e+04 ... 1e+04 1e+04
Data variables:
gravity (latitude, longitude) float64 19MB 9.801e+05 ... 9.802e+05
geoid (latitude, longitude) float64 19MB -29.5 -29.5 ... 15.4 15.4
topography (latitude, longitude) float64 19MB 2.742e+03 ... -4.237e+03
Attributes:
Conventions: CF-1.8
title: Gravity acceleration (EIGEN-6C4) at a constant geometric...
crs: WGS84
source: Generated from the EIGEN-6C4 model by the ICGEM Calculat...
license: Creative Commons Attribution 4.0 International Licence
references: https://doi.org/10.5880/icgem.2015.1
long_name: gravity acceleration
description: magnitude of the gravity acceleration vector (gravitatio...
units: mGal
actual_range: [974748.6 980201.9]
icgem_metadata: generating_institute: gfz-potsdam\ngenerating_date: 2021...
grdimage [WARNING]: Longitude range too small; geographic boundary condition changed to natural.
import boule as bl
import ensaio
import pygmt
import xarray as xr
import harmonica as hm
# Load the global gravity, topography, and geoid grids
fname_gravity = ensaio.fetch_earth_gravity(version=1)
fname_geoid = ensaio.fetch_earth_geoid(version=1)
fname_topo = ensaio.fetch_earth_topography(version=1)
data = xr.merge(
[
xr.load_dataarray(fname_gravity),
xr.load_dataarray(fname_geoid),
xr.load_dataarray(fname_topo),
]
)
print(data)
# Calculate normal gravity and the disturbance
ellipsoid = bl.WGS84
gamma = ellipsoid.normal_gravity(data.latitude, data.height)
disturbance = data.gravity - gamma
# Reference the topography to the ellipsoid
topography_ell = data.topography + data.geoid
# Calculate the Bouguer planar correction and the topography-free disturbance.
# Use the default densities for the crust and ocean water.
bouguer = hm.bouguer_correction(topography_ell)
disturbance_topofree = disturbance - bouguer
# Make a plot of data using PyGMT
fig = pygmt.Figure()
pygmt.grd2cpt(grid=disturbance_topofree, cmap="vik+h0", continuous=True)
title = "Topography-free (Bouguer) gravity disturbance of the Earth"
with pygmt.config(FONT_TITLE="14p"):
fig.grdimage(
region="g",
projection="G-60/0/15c",
frame=f"+t{title}",
grid=disturbance_topofree,
cmap=True,
)
fig.coast(shorelines="0.5p,black", resolution="crude")
fig.colorbar(cmap=True, frame=["a200f50", "x+lmGal"])
fig.show()
Total running time of the script: (0 minutes 6.537 seconds)