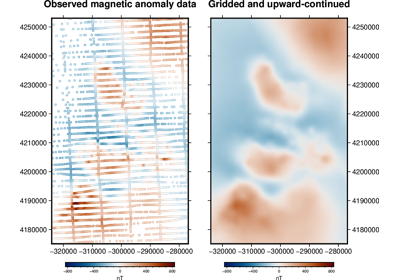
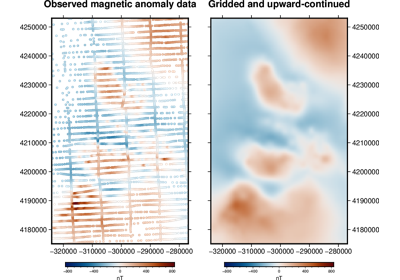
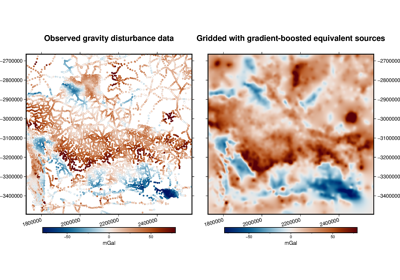
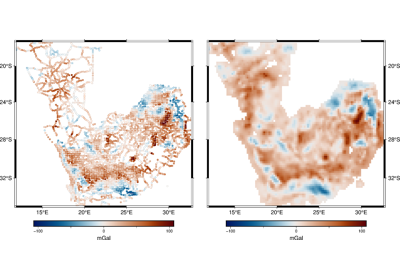
harmonica.EquivalentSources#
- class harmonica.EquivalentSources(damping=None, points=None, depth: float | str = 'default', block_size=None, parallel=True, dtype='float64')[source]#
Equivalent sources for generic harmonic functions (gravity, magnetics).
These equivalent sources can be used for:
Cartesian coordinates (geographic coordinates must be project before use)
Gravity and magnetic data (including derivatives)
Single data types
Interpolation
Upward continuation
Finite-difference based derivative calculations
They cannot be used for:
Regional or global data where Earth’s curvature must be taken into account
Joint inversion of multiple data types (e.g., gravity + gravity gradients)
Reduction to the pole of magnetic total field anomaly data
Analytical derivative calculations
By default, the point sources are located beneath the observed potential-field measurement points [Cordell1992] that are passed as arguments to the
EquivalentSources.fitmethod, producing the same number of sources as data points. Alternatively, we can reduce the number of sources by using block-averaged sources [Soler2021]: we divide the data region in blocks of equal size and compute the median location of the observations points that fall under each block. Then, we locate one point source beneath each one of these locations. The size of the blocks, that indirectly controls how many sources will be created, can be specified through theblock_sizeargument. We recommend choosing ablock_sizeno larger than the resolution of the grid where interpolations will be carried out.The depth of the sources can be controlled by the
depthargument. Each source is located beneath each data point or block-averaged location at a depth equal to its elevation minus the value of thedepth_attribute. If"default"is passed to thedepthargument, then thedepth_attribute is set to 4.5 times the mean distance between first neighboring sources. If a numerical value is passed to thedepthargument, then this is the one used for thedepth_attribute. A positive value ofdepth_locates sources _beneath_ the data points or the block-averaged locations, thus a negativedepth_will put the sources _above_ them.Custom source locations can be chosen by specifying the
pointsargument, in which case theblock_sizeanddeptharguments will be ignored.The corresponding coefficient for each point source is estimated through linear least-squares with damping (Tikhonov 0th order) regularization.
The Green’s function for point mass effects used is the inverse Euclidean distance between the observation points and the point sources:
\[\phi(\bar{x}, \bar{x}') = \frac{1}{||\bar{x} - \bar{x}'||}\]where \(\bar{x}\) and \(\bar{x}'\) are the coordinate vectors of the observation point and the source, respectively.
- Parameters:
- damping
Noneorfloat The positive damping regularization parameter. Controls how much smoothness is imposed on the estimated coefficients. If None, no regularization is used.
- points
Noneorlistofarrays(optional) List containing the coordinates of the equivalent point sources. Coordinates are assumed to be in the following order: (
easting,northing,upward). If None, will place one point source below each observation point at a fixed relative depth below the observation point [Cordell1992]. Defaults to None.- depth
floator “default” Parameter used to control the depth at which the point sources will be located. If a non-zero value is provided, each source is located beneath each data point (or block-averaged location) at a depth equal to its elevation minus the
depthvalue. If set to"default", the depth of the sources will be estimated as 4.5 times the mean distance between first neighboring sources. This parameter is ignored if points is specified. Defaults to"default".- block_size: float, tuple = (s_north, s_east) or None
Size of the blocks used on block-averaged equivalent sources. If a single value is passed, the blocks will have a square shape. Alternatively, the dimensions of the blocks in the South-North and West-East directions can be specified by passing a tuple. If None, no block-averaging is applied. This parameter is ignored if points are specified. Default to None.
- parallelbool
If True any predictions and Jacobian building is carried out in parallel through Numba’s
jit.prange, reducing the computation time. If False, these tasks will be run on a single CPU. Default to True.- dtypedata-type
The desired data-type for the predictions and the Jacobian matrix. Default to
"float64".
- damping
References
- Attributes:
- points_2d-array
Coordinates of the equivalent point sources.
- coefs_
array Estimated coefficients of every point source.
- depth_
floatorNone Estimated depth of the sources calculated as 4.5 times the mean distance between first neighboring sources. This attribute is set to None if
pointsis passed.- region_
tuple The boundaries (
[W, E, S, N]) of the data used to fit the interpolator. Used as the default region for thegridmethod.
Methods
filter(coordinates, data[, weights])Filter the data through the gridder and produce residuals.
fit(coordinates, data[, weights])Fit the coefficients of the equivalent sources.
Get metadata routing of this object.
get_params([deep])Get parameters for this estimator.
grid(coordinates[, dims, data_names, projection])Interpolate the data onto a regular grid.
jacobian(coordinates, points)Make the Jacobian matrix for the equivalent sources.
predict(coordinates)Evaluate the estimated equivalent sources on the given set of points.
profile(point1, point2, upward, size[, ...])Interpolate data along a profile between two points.
scatter([region, size, random_state, dims, ...])score(coordinates, data[, weights])Score the gridder predictions against the given data.
set_fit_request(*[, coordinates, data, weights])Request metadata passed to the
fitmethod.set_params(**params)Set the parameters of this estimator.
set_predict_request(*[, coordinates])Request metadata passed to the
predictmethod.set_score_request(*[, coordinates, data, ...])Request metadata passed to the
scoremethod.
- EquivalentSources.filter(coordinates, data, weights=None)#
Filter the data through the gridder and produce residuals.
Calls
fiton the data, evaluates the residuals (data - predicted data), and returns the coordinates, residuals, and weights.Not very useful by itself but this interface makes gridders compatible with other processing operations and is used by
verde.Chainto join them together (for example, so you can fit a spline on the residuals of a trend).- Parameters:
- coordinates
tupleofarrays Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). For the specific definition of coordinate systems and what these names mean, see the class docstring.
- data
arrayortupleofarrays The data values of each data point. If the data has more than one component, data must be a tuple of arrays (one for each component).
- weights
Noneorarrayortupleofarrays If not None, then the weights assigned to each data point. If more than one data component is provided, you must provide a weights array for each data component (if not None).
- coordinates
- Returns:
coordinates,residuals,weightsThe coordinates and weights are same as the input. Residuals are the input data minus the predicted data.
- EquivalentSources.fit(coordinates, data, weights=None)[source]#
Fit the coefficients of the equivalent sources.
The data region is captured and used as default for the
gridmethod.All input arrays must have the same shape.
- Parameters:
- coordinates
tupleofarrays Arrays with the coordinates of each data point. Should be in the following order: (
easting,northing,upward, …). Onlyeasting,northing, andupwardwill be used, all subsequent coordinates will be ignored.- data
array The data values of each data point.
- weights
Noneorarray If not None, then the weights assigned to each data point. Typically, this should be 1 over the data uncertainty squared.
- coordinates
- Returns:
selfReturns this estimator instance for chaining operations.
- EquivalentSources.get_metadata_routing()#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routing
MetadataRequest A
MetadataRequestencapsulating routing information.
- routing
- EquivalentSources.get_params(deep=True)#
Get parameters for this estimator.
- EquivalentSources.grid(coordinates, dims=None, data_names=None, projection=None, **kwargs)[source]#
Interpolate the data onto a regular grid.
The coordinates of the regular grid must be passed through the
coordinatesargument as a tuple containing three arrays in the following order:(easting, nothing, upward). They can be easily created through theverde.grid_coordinatesfunction. If the grid points must be all at the same height, it can be specified in theextra_coordsargument ofverde.grid_coordinates.Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output
xarray.Dataset. Default names will be provided if none are given.- Parameters:
- coordinates
tupleofarrays Tuple of arrays containing the coordinates of the grid in the following order: (easting, northing, upward). The easting and northing arrays could be 1d or 2d arrays, if they are 2d they must be part of a meshgrid. The upward array should be a 2d array with the same shape of easting and northing (if they are 2d arrays) or with a shape of
(northing.size, easting.size)(if they are 1d arrays).- dims
listorNone The names of the northing and easting data dimensions, respectively, in the output grid. Default is determined from the
dimsattribute of the class. Must be defined in the following order: northing dimension, easting dimension. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.- data_names
listofNone The name(s) of the data variables in the output grid. Defaults to
['scalars'].- projection
callableorNone If not None, then should be a callable object
projection(easting, northing) -> (proj_easting, proj_northing)that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated grid coordinates before passing them intopredict. For example, you can use this to generate a geographic grid from a Cartesian gridder.
- coordinates
- Returns:
- grid
xarray.Dataset The interpolated grid. Metadata about the interpolator is written to the
attrsattribute.
- grid
See also
- EquivalentSources.jacobian(coordinates, points)[source]#
Make the Jacobian matrix for the equivalent sources.
Each column of the Jacobian is the Green’s function for a single point source evaluated on all observation points.
- Parameters:
- coordinates
tupleofarrays Arrays with the coordinates of each data point. Should be in the following order: (
easting,northing,upward). Each array must be 1D.- points
tupleofarrays Tuple of arrays containing the coordinates of the equivalent point sources in the following order: (
easting,northing,upward). Each array must be 1D.
- coordinates
- Returns:
- jacobian2D
array The (n_data, n_points) Jacobian matrix.
- jacobian2D
- EquivalentSources.predict(coordinates)[source]#
Evaluate the estimated equivalent sources on the given set of points.
Requires a fitted estimator (see
fit).- Parameters:
- coordinates
tupleofarrays Arrays with the coordinates of each data point. Should be in the following order: (
easting,northing,upward, …). Onlyeasting,northingandupwardwill be used, all subsequent coordinates will be ignored.
- coordinates
- Returns:
- data
array The data values evaluated on the given points.
- data
- EquivalentSources.profile(point1, point2, upward, size, dims=None, data_names=None, projection=None, **kwargs)[source]#
Interpolate data along a profile between two points.
Generates the profile along a straight line assuming Cartesian distances and the same upward coordinate for all points. Point coordinates are generated by
verde.profile_coordinates. Other arguments for this function can be passed as extra keyword arguments (kwargs) to this method.Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output
pandas.DataFrame. Default names are provided.Includes the calculated Cartesian distance from point1 for each data point in the profile.
To specify point1 and point2 in a coordinate system that would require projection to Cartesian (geographic longitude and latitude, for example), use the
projectionargument. With this option, the input points will be projected using the given projection function prior to computations. The generated Cartesian profile coordinates will be projected back to the original coordinate system. Note that the profile points are evenly spaced in projected coordinates, not the original system (e.g., geographic).- Parameters:
- point1
tuple The easting and northing coordinates, respectively, of the first point.
- point2
tuple The easting and northing coordinates, respectively, of the second point.
- upward
float Upward coordinate of the profile points.
- size
int The number of points to generate.
- dims
listorNone The names of the northing and easting data dimensions, respectively, in the output dataframe. Default is determined from the
dimsattribute of the class. Must be defined in the following order: northing dimension, easting dimension. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.- data_names
listofNone The name(s) of the data variables in the output dataframe. Defaults to
['scalars']for scalar data,['east_component', 'north_component']for 2D vector data, and['east_component', 'north_component', 'vertical_component']for 3D vector data.- projection
callableorNone If not None, then should be a callable object
projection(easting, northing, inverse=False) -> (proj_easting, proj_northing)that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. Should also take an optional keyword argumentinverse(default to False) that if True will calculate the inverse transform instead. This function will be used to project the profile end points before generating coordinates and passing them intopredict. It will also be used to undo the projection of the coordinates before returning the results.
- point1
- Returns:
- table
pandas.DataFrame The interpolated values along the profile.
- table
- EquivalentSources.scatter(region=None, size=300, random_state=0, dims=None, data_names=None, projection=None, **kwargs)[source]#
Warning
Not implemented method. The scatter method will be deprecated on Verde v2.0.0.
- EquivalentSources.score(coordinates, data, weights=None)#
Score the gridder predictions against the given data.
Calculates the R^2 coefficient of determination of between the predicted values and the given data values. A maximum score of 1 means a perfect fit. The score can be negative.
Warning
The default scoring will change from R² to negative root mean squared error (RMSE) in Verde 2.0.0. This may change model selection results slightly. The negative version will be used to maintain the behaviour of larger scores being better, which is more compatible with current model selection code.
If the data has more than 1 component, the scores of each component will be averaged.
- Parameters:
- coordinates
tupleofarrays Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). For the specific definition of coordinate systems and what these names mean, see the class docstring.
- data
arrayortupleofarrays The data values of each data point. If the data has more than one component, data must be a tuple of arrays (one for each component).
- weights
Noneorarrayortupleofarrays If not None, then the weights assigned to each data point. If more than one data component is provided, you must provide a weights array for each data component (if not None).
- coordinates
- Returns:
- score
float The R^2 score
- score
- EquivalentSources.set_fit_request(*, coordinates: bool | None | str = '$UNCHANGED$', data: bool | None | str = '$UNCHANGED$', weights: bool | None | str = '$UNCHANGED$') EquivalentSources#
Request metadata passed to the
fitmethod.Note that this method is only relevant if
enable_metadata_routing=True(seesklearn.set_config). Please see User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed tofitif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it tofit.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.New in version 1.3.
Note
This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a
Pipeline. Otherwise it has no effect.- Parameters:
- coordinates
str,True,False,orNone, default=sklearn.utils.metadata_routing.UNCHANGED Metadata routing for
coordinatesparameter infit.- data
str,True,False,orNone, default=sklearn.utils.metadata_routing.UNCHANGED Metadata routing for
dataparameter infit.- weights
str,True,False,orNone, default=sklearn.utils.metadata_routing.UNCHANGED Metadata routing for
weightsparameter infit.
- coordinates
- Returns:
- self
object The updated object.
- self
- EquivalentSources.set_params(**params)#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **params
dict Estimator parameters.
- **params
- Returns:
- self
estimatorinstance Estimator instance.
- self
- EquivalentSources.set_predict_request(*, coordinates: bool | None | str = '$UNCHANGED$') EquivalentSources#
Request metadata passed to the
predictmethod.Note that this method is only relevant if
enable_metadata_routing=True(seesklearn.set_config). Please see User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed topredictif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it topredict.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.New in version 1.3.
Note
This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a
Pipeline. Otherwise it has no effect.
- EquivalentSources.set_score_request(*, coordinates: bool | None | str = '$UNCHANGED$', data: bool | None | str = '$UNCHANGED$', weights: bool | None | str = '$UNCHANGED$') EquivalentSources#
Request metadata passed to the
scoremethod.Note that this method is only relevant if
enable_metadata_routing=True(seesklearn.set_config). Please see User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.New in version 1.3.
Note
This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a
Pipeline. Otherwise it has no effect.- Parameters:
- coordinates
str,True,False,orNone, default=sklearn.utils.metadata_routing.UNCHANGED Metadata routing for
coordinatesparameter inscore.- data
str,True,False,orNone, default=sklearn.utils.metadata_routing.UNCHANGED Metadata routing for
dataparameter inscore.- weights
str,True,False,orNone, default=sklearn.utils.metadata_routing.UNCHANGED Metadata routing for
weightsparameter inscore.
- coordinates
- Returns:
- self
object The updated object.
- self