Toggle navigation

.rst .pdf

repository open issue suggest edit

Tesseroids (spherical prisms)

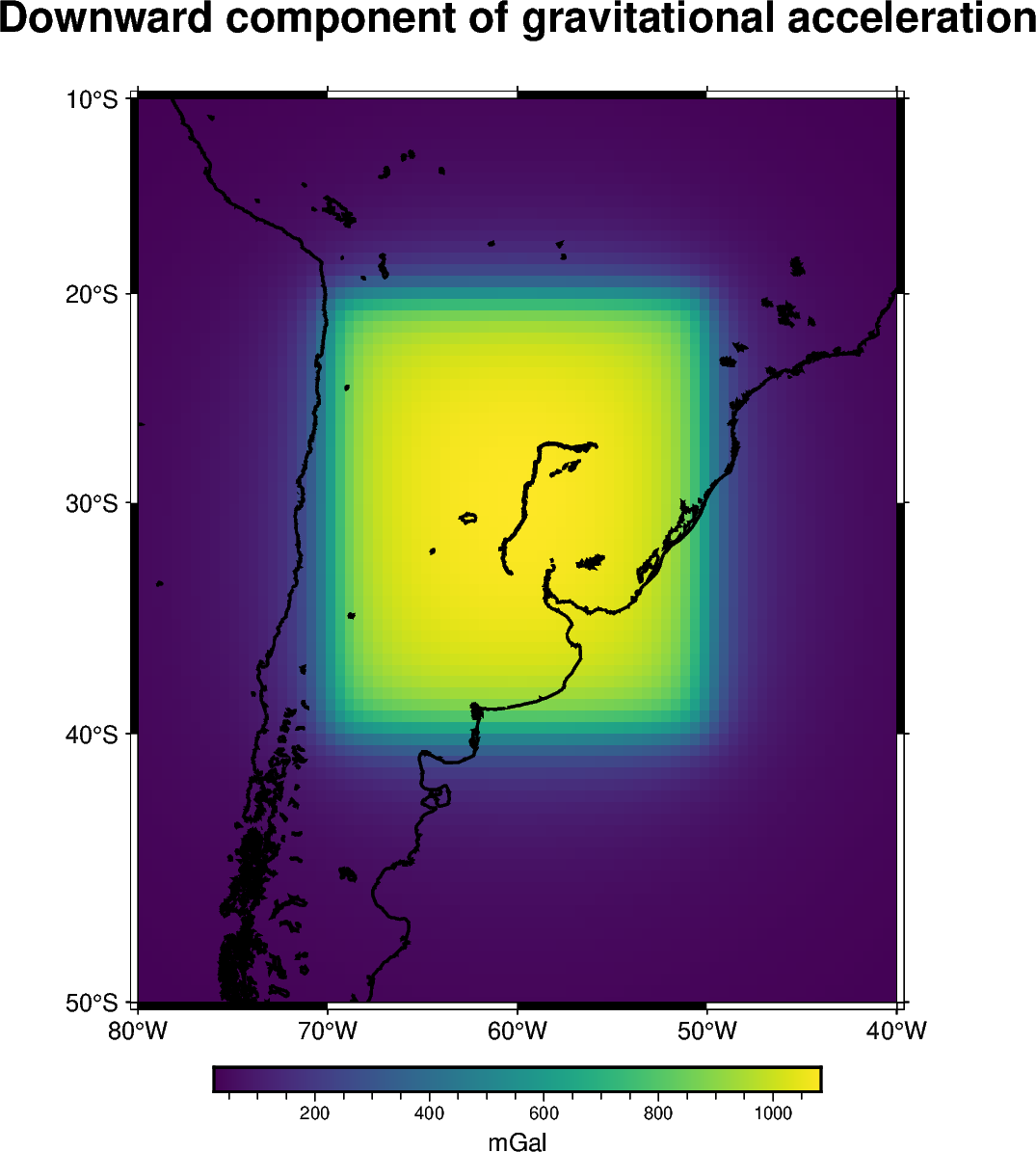
Computing the gravitational fields generated by regional or global scale structures require to take into account the curvature of the Earth. One common approach is to use spherical prisms also known as tesseroids. We will compute the downward component of the gravitational acceleration generated by a single tesseroid on a computation grid through the harmonica.tesseroid_gravity function.

Out:

[[26.25264292 26.6161005  26.98494351 ... 26.98494351 26.6161005
  26.25264292]
 [26.82151989 27.2134279  27.61202586 ... 27.61202586 27.2134279
  26.82151989]
 [27.41031127 27.8332173  28.26436726 ... 28.26436726 27.8332173
  27.41031127]
 ...
 [24.3828477  24.83864142 25.30833989 ... 25.30833989 24.83864142
  24.3828477 ]
 [23.90092716 24.33039969 24.77197999 ... 24.77197999 24.33039969
  23.90092716]
 [23.43483023 23.83981484 24.25533515 ... 24.25533515 23.83981484
  23.43483023]]
<IPython.core.display.Image object>

import boule as bl
import pygmt
import verde as vd

import harmonica as hm

# Use the WGS84 ellipsoid to obtain the mean Earth radius which we'll use to
# reference the tesseroid
ellipsoid = bl.WGS84

# Define tesseroid with top surface at the mean Earth radius, thickness of 10km
# (bottom = top - thickness) and density of 2670kg/m^3
tesseroid = [-70, -50, -40, -20, ellipsoid.mean_radius - 10e3, ellipsoid.mean_radius]
density = 2670

# Define computation points on a regular grid at 100km above the mean Earth
# radius
coordinates = vd.grid_coordinates(
    region=[-80, -40, -50, -10],
    shape=(80, 80),
    extra_coords=100e3 + ellipsoid.mean_radius,
)

# Compute the radial component of the acceleration
gravity = hm.tesseroid_gravity(coordinates, tesseroid, density, field="g_z")
print(gravity)
grid = vd.make_xarray_grid(
    coordinates, gravity, data_names="gravity", extra_coords_names="extra"
)

# Plot the gravitational field
fig = pygmt.Figure()

title = "Downward component of gravitational acceleration"

with pygmt.config(FONT_TITLE="16p"):
    fig.grdimage(
        region=[-80, -40, -50, -10],
        projection="M-60/-30/10c",
        grid=grid.gravity,
        frame=["a", f"+t{title}"],
        cmap="viridis",
    )

fig.colorbar(cmap=True, frame=["a200f50", "x+lmGal"])

fig.coast(shorelines="1p,black")

fig.show()

previous

Gravitational effect of topography

next

Layer of tesseroids