Toggle navigation

.rst .pdf

repository open issue suggest edit

Gridding in spherical coordinates

The curvature of the Earth must be taken into account when gridding and processing magnetic or gravity data on large regions. In these cases, projecting the data may introduce errors due to the distortions caused by the projection.

harmonica.EquivalentSourcesSph implements the equivalent sources technique in spherical coordinates. It has the same advantages as the Cartesian equivalent sources (harmonica.EquivalentSources) while taking into account the curvature of the Earth.

Out:

R² score: 0.9999999999905889

Generated grid:
 <xarray.Dataset>
Dimensions:              (spherical_latitude: 88, longitude: 105)
Coordinates:
  * longitude            (longitude) float64 11.91 12.11 12.31 ... 32.48 32.68
  * spherical_latitude   (spherical_latitude) float64 -34.76 -34.56 ... -17.28
    radius               (spherical_latitude, longitude) float64 6.378e+06 .....
Data variables:
    gravity_disturbance  (spherical_latitude, longitude) float64 6.019 ... 4.017
Attributes:
    metadata:  Generated by EquivalentSourcesSph(damping=0.001, relative_dept...
<IPython.core.display.Image object>

import boule as bl
import ensaio
import numpy as np
import pandas as pd
import pygmt
import verde as vd

import harmonica as hm

# Fetch the sample gravity data from South Africa
fname = ensaio.fetch_southern_africa_gravity(version=1)
data = pd.read_csv(fname)

# Downsample the data using a blocked mean to speed-up the computations
# for this example. This is preferred over simply discarding points to avoid
# aliasing effects.
blocked_mean = vd.BlockReduce(np.mean, spacing=0.2, drop_coords=False)
(longitude, latitude, elevation), gravity_data = blocked_mean.filter(
    (data.longitude, data.latitude, data.height_sea_level_m),
    data.gravity_mgal,
)

# Compute gravity disturbance by removing the gravity of normal Earth
ellipsoid = bl.WGS84
gamma = ellipsoid.normal_gravity(latitude, height=elevation)
gravity_disturbance = gravity_data - gamma

# Convert data coordinates from geodetic (longitude, latitude, height) to
# spherical (longitude, spherical_latitude, radius).
coordinates = ellipsoid.geodetic_to_spherical(longitude, latitude, elevation)

# Create the equivalent sources
eqs = hm.EquivalentSourcesSph(damping=1e-3, relative_depth=10000)

# Fit the sources coefficients to the observed magnetic anomaly
eqs.fit(coordinates, gravity_disturbance)

# Evaluate the data fit by calculating an R² score against the observed data.
# This is a measure of how well the sources fit the data, NOT how good the
# interpolation will be.
print("R² score:", eqs.score(coordinates, gravity_disturbance))

# Interpolate data on a regular grid with 0.2 degrees spacing. The
# interpolation requires the radius of the grid points (upward coordinate). By
# passing in the maximum radius of the data, we're effectively
# upward-continuing the data. The grid will be defined in spherical
# coordinates.
region = vd.get_region(coordinates)  # get the region boundaries
upward = coordinates[-1].max()
grid_coords = vd.grid_coordinates(region=region, spacing=0.2, extra_coords=upward)
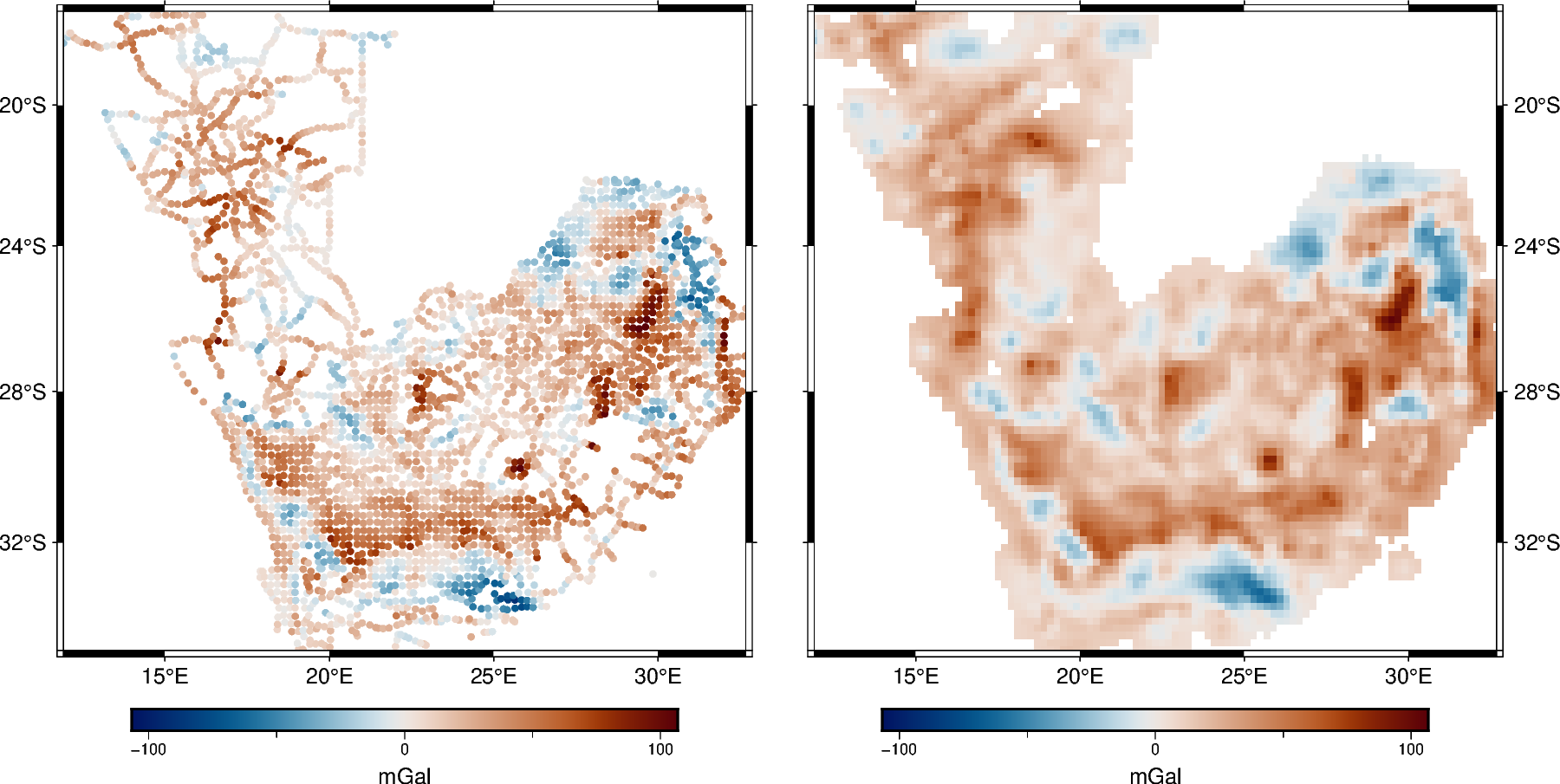
grid = eqs.grid(coordinates=grid_coords, data_names=["gravity_disturbance"])

# The grid is a xarray.Dataset with values, coordinates, and metadata
print("\nGenerated grid:\n", grid)

# Mask grid points too far from data points
grid = vd.distance_mask(data_coordinates=coordinates, maxdist=0.5, grid=grid)

# Plot observed and gridded gravity disturbance
fig = pygmt.Figure()

# Make colormap of data
# Get the 90% of the maximum absolute value between the original and gridded
# data so we can use the same color scale for both plots and have 0 centered
# at the white color.
maxabs = vd.maxabs(gravity_disturbance, grid.gravity_disturbance.values) * 0.90
pygmt.makecpt(
    cmap="vik",
    series=(-maxabs, maxabs),
    background=True,
)

fig.plot(
    projection="M10c",
    region=region,
    frame=["WSne", "xa5", "ya4"],
    x=longitude,
    y=latitude,
    color=gravity_disturbance,
    style="c0.1c",
    cmap=True,
)

fig.colorbar(cmap=True, frame=["a100f50", "x+lmGal"])

fig.shift_origin(xshift="w+3c")

fig.grdimage(
    frame=["ESnw", "xa5", "ya4"],
    grid=grid.gravity_disturbance,
    cmap=True,
)

fig.colorbar(cmap=True, frame=["a100f50", "x+lmGal"])

fig.show()

previous

Gradient-boosted equivalent sources

next

Point Masses in Cartesian Coordinates