Tesseroids#
When our region of interest covers several longitude and latitude degrees, utilizing Cartesian coordinates to model geological structures might introduce significant errors: they don’t take into account the curvature of the Earth. Instead, we would need to work in Spherical coordinates. A common approach to forward model bodies in geocentric spherical coordinates is to make use of tesseroids.
A tesseroid (a.k.a spherical prism) is a three dimensional body defined by the volume contained by two longitudinal boundaries, two latitudinal boundaries and the surfaces of two concentric spheres of different radii (see Figure: Tesseroid).
Figure: Tesseroid#
Tesseroid defined by two longitude coordinates (\(\lambda_1\) and \(\lambda_2\)), two latitude coordinates (\(\phi_1\) and \(\phi_2\)) and the surfaces of two concentric spheres of radii \(r_1\) and \(r_2\). This figure is a modified version of [Uieda2015].
Through the harmonica.tesseroid_gravity function we can calculate the
gravitational field of any tesseroid with a given density on any computation
point. Each tesseroid can be represented through a tuple containing its six
boundaries in the following order: west, east, south, north, bottom,
top, where the former four are its longitudinal and latitudinal boundaries in
decimal degrees and the latter two are the two radii given in meters.
Note
The harmonica.tesseroid_gravity numerically computed the
gravitational fields of tesseroids by applying a method that applies the
Gauss-Legendre Quadrature along with a bidimensional adaptive discretization
algorithm. Refer to [Soler2019] for more details.
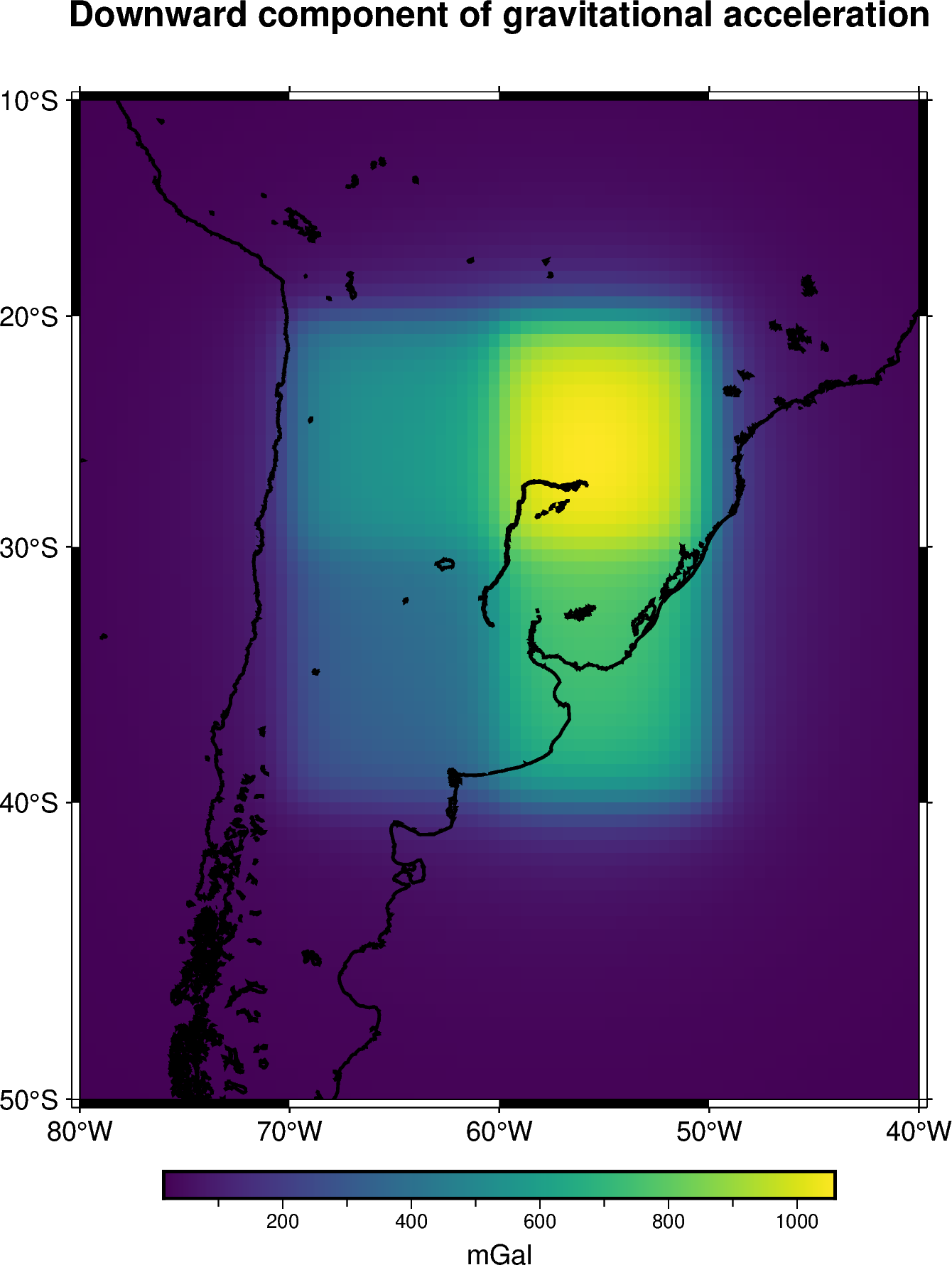
Lets define a single tesseroid and compute the gravitational potential it generates on a regular grid of computation points located at 10 km above its top boundary.
Get the WGS84 reference ellipsoid from boule so we can obtain its mean
radius:
import boule as bl
ellipsoid = bl.WGS84
mean_radius = ellipsoid.mean_radius
Define the tesseroid and its density (in kg per cubic meters):
tesseroid = (-70, -50, -40, -20, mean_radius - 10e3, mean_radius)
density = 2670
Define a set of computation points located on a regular grid at 100 km above the top surface of the tesseroid:
import verde as vd
coordinates = vd.grid_coordinates(
region=[-80, -40, -50, -10],
shape=(80, 80),
extra_coords=100e3 + mean_radius,
)
Lets compute the downward component of the gravitational acceleration it generates on the computation point:
import harmonica as hm
gravity = hm.tesseroid_gravity(coordinates, tesseroid, density, field="g_z")
Important
The downward component \(g_z\) of the gravitational acceleration computed in spherical coordinates corresponds to \(-g_r\), where \(g_r\) is the radial component.
And finally plot the computed gravitational field
import pygmt
grid = vd.make_xarray_grid(
coordinates, gravity, data_names="gravity", extra_coords_names="extra")
fig = pygmt.Figure()
title = "Downward component of gravitational acceleration"
with pygmt.config(FONT_TITLE="12p"):
fig.grdimage(
region=[-80, -40, -50, -10],
projection="M-60/-30/10c",
grid=grid.gravity,
frame=["a", f"+t{title}"],
cmap="viridis",
)
fig.colorbar(cmap=True, frame=["a200f50", "x+lmGal"])
fig.coast(shorelines="1p,black")
fig.show()
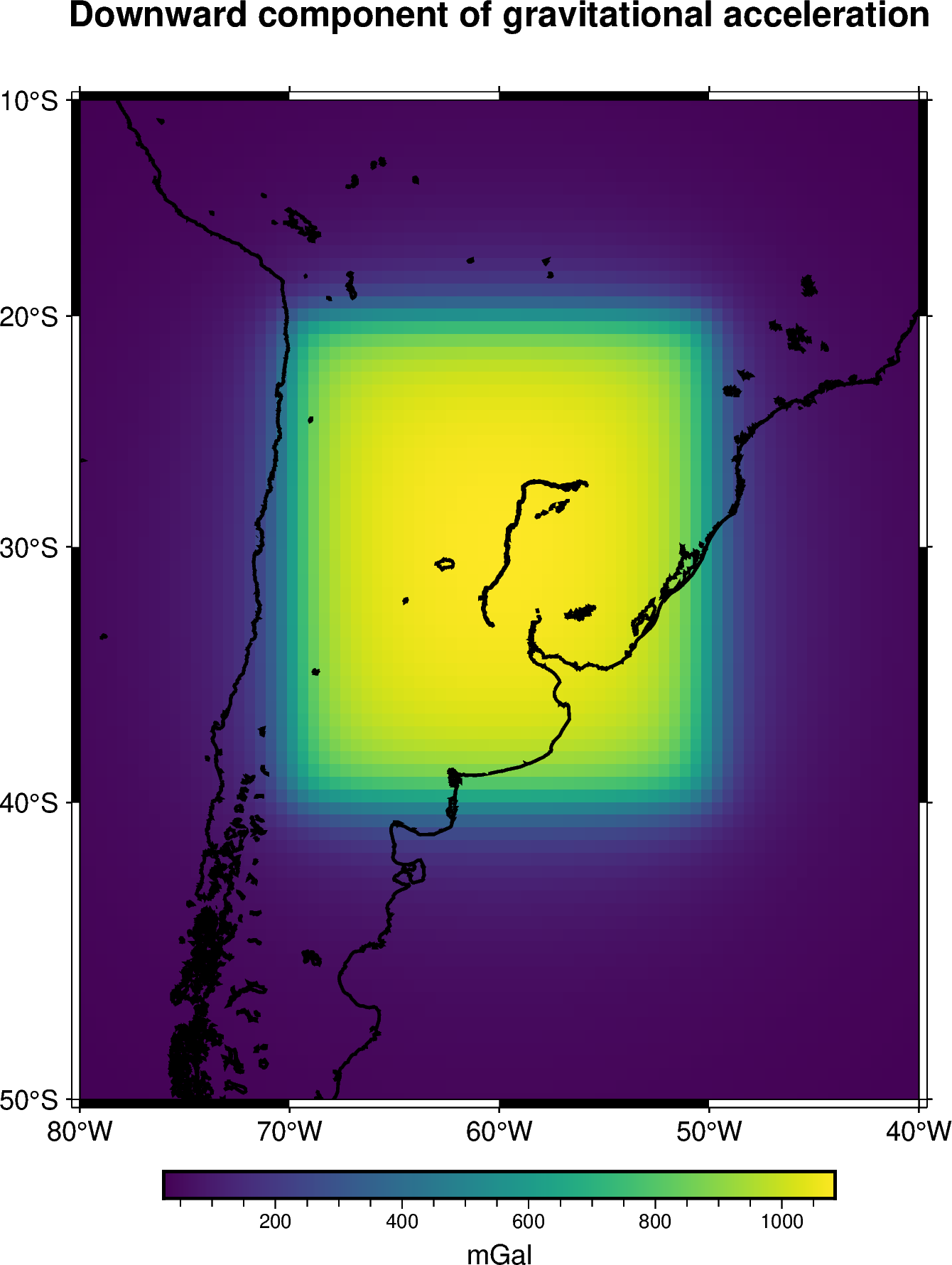
Multiple tesseroids#
We can compute the gravitational field of a set of tesseroids by passing a list
of them, where each tesseroid is defined as mentioned before, and then making
a single call of the harmonica.tesseroid_gravity function.
Lets define a set of four prisms along with their densities:
tesseroids = [
[-70, -65, -40, -35, mean_radius - 100e3, mean_radius],
[-55, -50, -40, -35, mean_radius - 100e3, mean_radius],
[-70, -65, -25, -20, mean_radius - 100e3, mean_radius],
[-55, -50, -25, -20, mean_radius - 100e3, mean_radius],
]
densities = [2670 , 2670, 2670, 2670]
Compute their gravitational effect on a grid of computation points:
coordinates = vd.grid_coordinates(
region=[-80, -40, -50, -10],
shape=(80, 80),
extra_coords=100e3 + mean_radius,
)
gravity = hm.tesseroid_gravity(coordinates, tesseroids, densities, field="g_z")
And plot the results:
grid = vd.make_xarray_grid(
coordinates, gravity, data_names="gravity", extra_coords_names="extra")
fig = pygmt.Figure()
title = "Downward component of gravitational acceleration"
with pygmt.config(FONT_TITLE="12p"):
fig.grdimage(
region=[-80, -40, -50, -10],
projection="M-60/-30/10c",
grid=grid.gravity,
frame=["a", f"+t{title}"],
cmap="viridis",
)
fig.colorbar(cmap=True, frame=["a1000f500", "x+lmGal"])
fig.coast(shorelines="1p,black")
fig.show()

Tesseroids with variable density#
The harmonica.tesseroid_gravity is capable of computing the
gravitational effects of tesseroids whose density is defined through
a continuous function of the radial coordinate. This is achieved by the
application of the method introduced in [Soler2021].
To do so we need to define a regular Python function for the density, which
should have a single argument (the radius coordinate) and return the
density of the tesseroids at that radial coordinate.
In addition, we need to decorate the density function with
numba.jit(nopython=True) or numba.njit for short.
Lets compute the gravitational effect of four tesseroids whose densities are
given by a custom linear density function.
Start by defining the tesseroids
tesseroids = (
[-70, -60, -40, -30, mean_radius - 3e3, mean_radius],
[-70, -60, -30, -20, mean_radius - 5e3, mean_radius],
[-60, -50, -40, -30, mean_radius - 7e3, mean_radius],
[-60, -50, -30, -20, mean_radius - 10e3, mean_radius],
)
Then, define a linear density function. We need to use the jit decorator so
Numba can run the forward model efficiently.
from numba import njit
@njit
def density(radius):
"""Linear density function"""
top = mean_radius
bottom = mean_radius - 10e3
density_top = 2670
density_bottom = 3000
slope = (density_top - density_bottom) / (top - bottom)
return slope * (radius - bottom) + density_bottom
Lets create a set of computation points located on a regular grid at 100km above the mean Earth radius:
coordinates = vd.grid_coordinates(
region=[-80, -40, -50, -10],
shape=(80, 80),
extra_coords=100e3 + ellipsoid.mean_radius,
)
And compute the gravitational fields the tesseroids generate:
gravity = hm.tesseroid_gravity(coordinates, tesseroids, density, field="g_z")
Finally, lets plot it:
grid = vd.make_xarray_grid(
coordinates, gravity, data_names="gravity", extra_coords_names="extra")
fig = pygmt.Figure()
title = "Downward component of gravitational acceleration"
with pygmt.config(FONT_TITLE="12p"):
fig.grdimage(
region=[-80, -40, -50, -10],
projection="M-60/-30/10c",
grid=grid.gravity,
frame=["a", f"+t{title}"],
cmap="viridis",
)
fig.colorbar(cmap=True, frame=["a200f100", "x+lmGal"])
fig.coast(shorelines="1p,black")
fig.show()