Gravity Disturbance#

Gravity disturbances are the differences between the measured gravity and a reference (normal) gravity produced by an ellipsoid:

δ g (p) = g (p) - γ (p)

Where $δ g$ is the gravity disturbance, $g$ the measured gravity, $γ$ is the normal gravity and $p$ is the observation point where the gravity measurement has been carried out. The disturbances are what allows geoscientists to infer the internal structure of the Earth.

Tip

The measured gravity $g$ is defined as the module of the gravity acceleration, i.e. the module of the gradient of Earth’s gravity potential $W$ , which includes both the gravitational potential $V$ (due to the gravitational attraction of the masses that composes the Earth) and the centrifugal potential $Φ$ due to Earth’s rotation

W = V + Φ

Tip

The normal gravity $γ$ is defined as the gradient of the potential gravity field generated by the reference ellipsoid $U$ composed by the sum of the gravitational field $V_{ell}$ and the centrifugal potential $Φ$ :

U = V_{ell} + Φ

See also

See [Hofmann-WellenhofMoritz2006] for detailed explainations of Earth gravity and the definition of its gravity and gravitational potentials.

We can compute the normal gravity generated by any ellipsoid through the boule.Ellipsoid.normal_gravity method from boule and then use it to compute gravity disturbances.

Lets start by loading a sample gravity dataset for the whole Earth:

import ensaio
import xarray as xr

fname = ensaio.fetch_earth_gravity(version=1)
gravity = xr.load_dataarray(fname)
print(gravity)

<xarray.DataArray 'gravity' (latitude: 1081, longitude: 2161)> Size: 19MB
array([[980106.525, 980106.525, 980106.525, ..., 980106.525, 980106.525,
        980106.525],
       [980108.225, 980108.225, 980108.225, ..., 980108.225, 980108.225,
        980108.225],
       [980108.825, 980108.825, 980108.825, ..., 980108.725, 980108.725,
        980108.825],
       ...,
       [980153.825, 980153.725, 980153.625, ..., 980153.925, 980153.825,
        980153.825],
       [980160.425, 980160.425, 980160.425, ..., 980160.425, 980160.425,
        980160.425],
       [980157.525, 980157.525, 980157.525, ..., 980157.525, 980157.525,
        980157.525]], shape=(1081, 2161))
Coordinates:
  * longitude  (longitude) float64 17kB -180.0 -179.8 -179.7 ... 179.8 180.0
  * latitude   (latitude) float64 9kB -90.0 -89.83 -89.67 ... 89.67 89.83 90.0
    height     (latitude, longitude) float32 9MB 1e+04 1e+04 ... 1e+04 1e+04
Attributes:
    Conventions:     CF-1.8
    title:           Gravity acceleration (EIGEN-6C4) at a constant geometric...
    crs:             WGS84
    source:          Generated from the EIGEN-6C4 model by the ICGEM Calculat...
    license:         Creative Commons Attribution 4.0 International Licence
    references:      https://doi.org/10.5880/icgem.2015.1
    long_name:       gravity acceleration
    description:     magnitude of the gravity acceleration vector (gravitatio...
    units:           mGal
    actual_range:    [974748.6 980201.9]
    icgem_metadata:  generating_institute: gfz-potsdam\ngenerating_date: 2021...

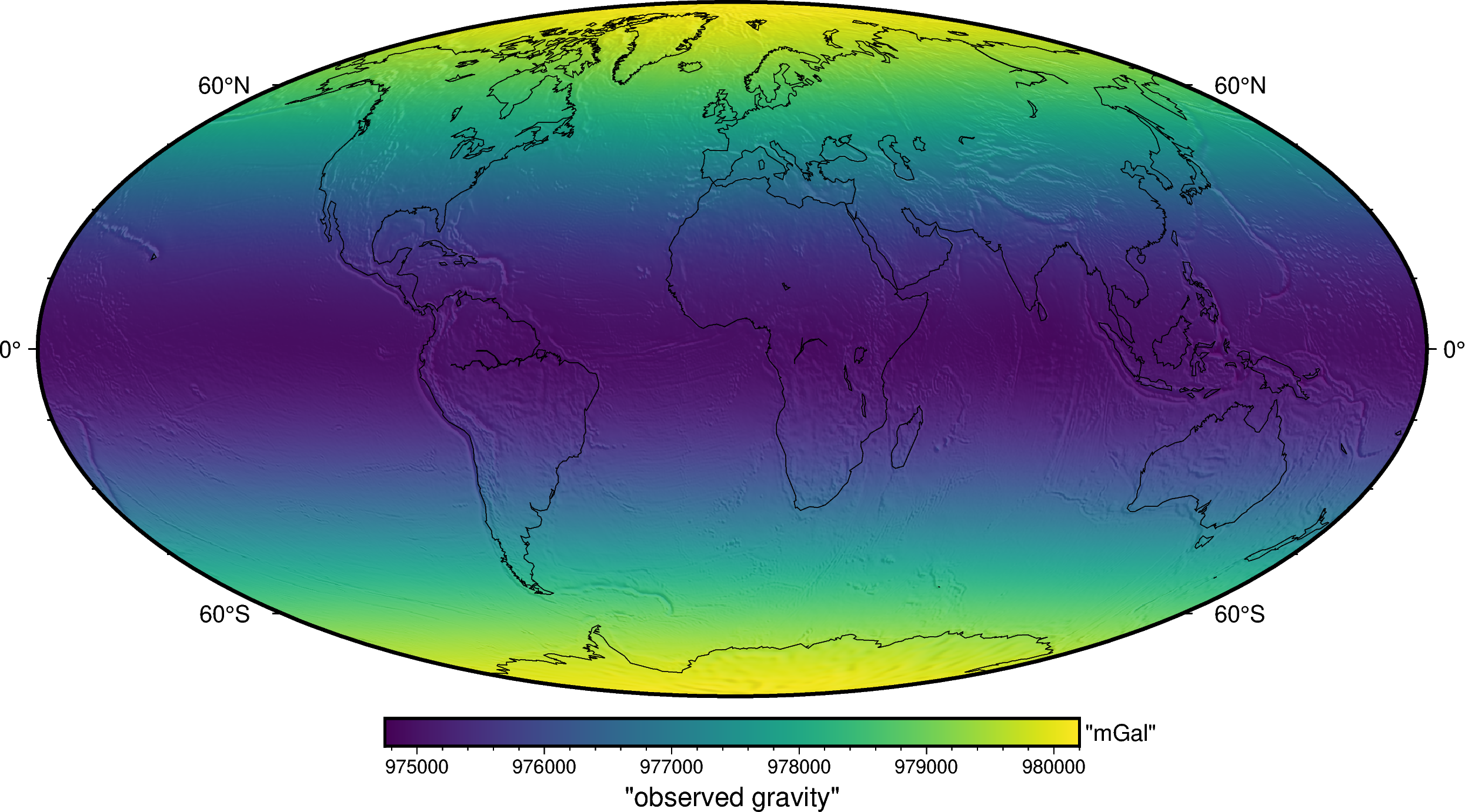
These observations are located on a regular grid on geodetic coordinates at the same height of 10 km above the reference ellipsoid. Lets plot it:

import pygmt

fig = pygmt.Figure()
fig.grdimage(
    gravity,
    projection="W20c",
    cmap="viridis",
    shading="+a45+nt0.2",
)
fig.basemap(frame=["af", "WEsn"])
fig.colorbar(
    position="JCB+w10c",
    frame=["af", 'y+l"mGal"', 'x+l"observed gravity"'],
)
fig.coast(shorelines=True, resolution="c", area_thresh=1e4)
fig.show()

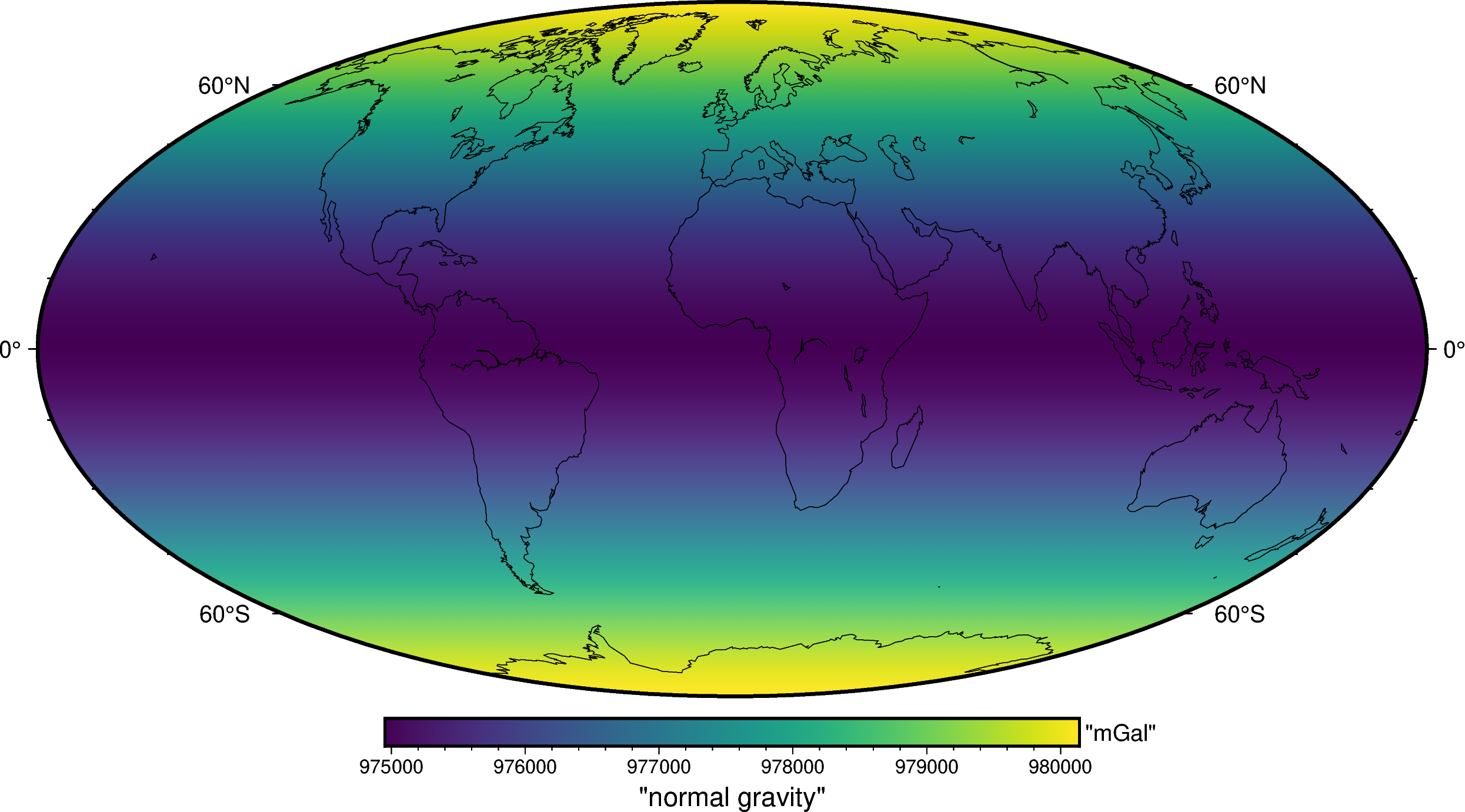
We can then get the WGS84 ellipsoid defined in boule and use the boule.Ellipsoid.normal_gravity to compute the normal gravity (the gravity acceleration generated by the ellipsoid) on every observation point. This method implements the closed-form formula of [LiGotze2001], which calculates the normal gravity at any latitude and (geometric) height through an analytic solution.

import boule as bl

ellipsoid = bl.WGS84
normal_gravity = ellipsoid.normal_gravity(gravity.latitude, gravity.height)

And plot it:

fig = pygmt.Figure()
fig.grdimage(
    normal_gravity,
    projection="W20c",
    cmap="viridis",
    shading="+a45+nt0.2",
)
fig.basemap(frame=["af", "WEsn"])
fig.colorbar(
    position="JCB+w10c",
    frame=["af", 'y+l"mGal"', 'x+l"normal gravity"'],
)
fig.coast(shorelines=True, resolution="c", area_thresh=1e4)
fig.show()

Now we can compute the gravity disturbance:

gravity_disturbance = gravity - normal_gravity
print(gravity_disturbance)

<xarray.DataArray (latitude: 1081, longitude: 2161)> Size: 19MB
array([[-35.81009235, -35.81009235, -35.81009235, ..., -35.81009235,
        -35.81009235, -35.81009235],
       [-34.06597894, -34.06597894, -34.06597894, ..., -34.06597894,
        -34.06597894, -34.06597894],
       [-33.33364042, -33.33364042, -33.33364042, ..., -33.43364042,
        -33.43364042, -33.33364042],
       ...,
       [ 11.66635958,  11.56635958,  11.46635958, ...,  11.76635958,
         11.66635958,  11.66635958],
       [ 18.13402106,  18.13402106,  18.13402106, ...,  18.13402106,
         18.13402106,  18.13402106],
       [ 15.18990765,  15.18990765,  15.18990765, ...,  15.18990765,
         15.18990765,  15.18990765]], shape=(1081, 2161))
Coordinates:
  * longitude  (longitude) float64 17kB -180.0 -179.8 -179.7 ... 179.8 180.0
  * latitude   (latitude) float64 9kB -90.0 -89.83 -89.67 ... 89.67 89.83 90.0
    height     (latitude, longitude) float32 9MB 1e+04 1e+04 ... 1e+04 1e+04

And plot it:

import verde as vd

maxabs = vd.maxabs(gravity_disturbance)

fig = pygmt.Figure()
pygmt.makecpt(series=[-maxabs, maxabs], cmap="polar+h")
fig.grdimage(
    gravity_disturbance,
    projection="W20c",
    cmap=True,
    shading="+a45+nt0.2",
)
fig.basemap(frame=["af", "WEsn"])
fig.colorbar(
    position="JCB+w10c",
    frame=["af", 'y+l"mGal"', 'x+l"gravity disturbance"'],
)
fig.coast(shorelines=True, resolution="c", area_thresh=1e4)
fig.show()

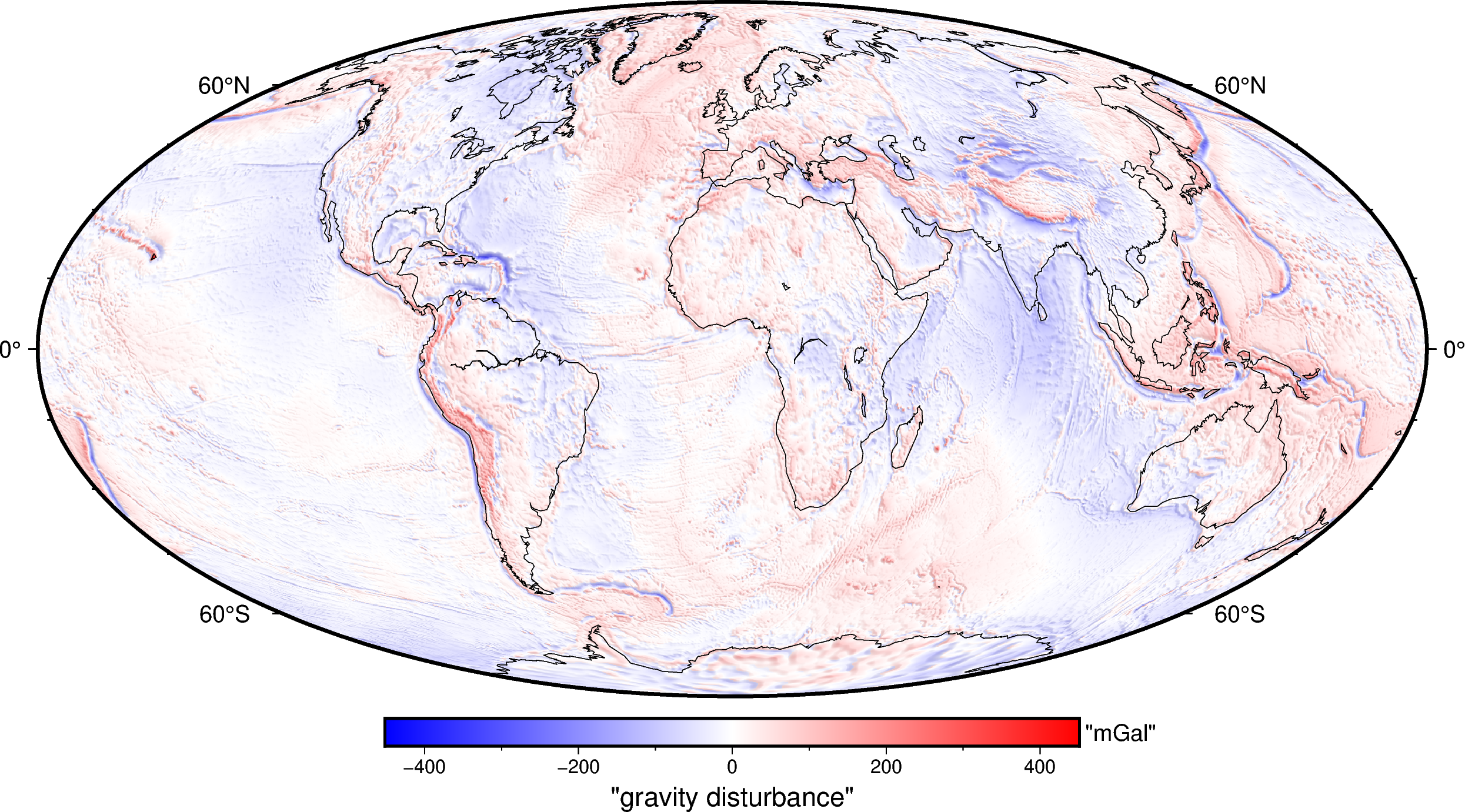
The gravity disturbances can be interpreted as the gravitational effect of every anomalous mass, i.e. that is not contained in the normal Earth.

Download Python script

Download Jupyter notebook