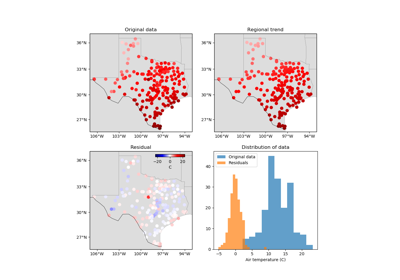
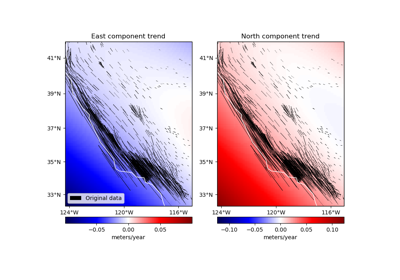
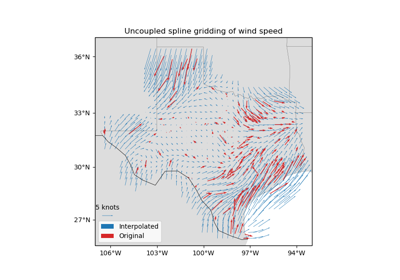
verde.Trend¶

class verde.Trend(degree)[source]¶

Fit a 2D polynomial trend to spatial data.

The polynomial of degree \(N\) is defined as:

\[f(e, n) = \sum\limits_{l=0}^{N}\sum\limits_{m=0}^{N - l} e^l n^m\]

in which \(e\) and \(n\) are the easting and northing coordinates, respectively.

The trend is estimated through weighted least-squares regression. The Jacobian (design, sensitivity, feature, etc) matrix for the regression is normalized using sklearn.preprocessing.StandardScaler without centering the mean so that the transformation can be undone in the estimated coefficients.

Parameters

degree (int) – The degree of the polynomial. Must be >= 0 (a degree of zero would estimate the mean of the data).

Variables

coef_ (array) – The estimated polynomial coefficients that fit the observed data.
region_ (tuple) – The boundaries ([W, E, S, N]) of the data used to fit the interpolator. Used as the default region for the grid and scatter methods.

Examples

>>> from verde import grid_coordinates
>>> import numpy as np
>>> coordinates = grid_coordinates((1, 5, -5, -1), shape=(5, 5))
>>> data = 10 + 2*coordinates[0] - 0.4*coordinates[1]
>>> trend = Trend(degree=1).fit(coordinates, data)
>>> print(
...     "Coefficients:",
...     ', '.join(['{:.1f}'.format(i) for i in trend.coef_])
... )
Coefficients: 10.0, 2.0, -0.4
>>> np.allclose(trend.predict(coordinates), data)
True

A zero degree polynomial estimates the mean of the data:

>>> mean = Trend(degree=0).fit(coordinates, data)
>>> np.allclose(mean.predict(coordinates), data.mean())
True
>>> print("Data mean:", '{:.2f}'.format(data.mean()))
Data mean: 17.20
>>> print("Coefficient:", '{:.2f}'.format(mean.coef_[0]))
Coefficient: 17.20

We can use weights to account for outliers or data points with variable uncertainties (see verde.variance_to_weights):

>>> data_out = data.copy()
>>> data_out[2, 2] += 500
>>> weights = np.ones_like(data)
>>> weights[2, 2] = 1e-10
>>> trend_out = Trend(degree=1).fit(coordinates, data_out, weights)
>>> # Still recover the coefficients even with the added outlier
>>> print(
...     "Coefficients:",
...     ', '.join(['{:.1f}'.format(i) for i in trend_out.coef_])
... )
Coefficients: 10.0, 2.0, -0.4
>>> # The residual at the outlier location should be values we added to
>>> # that point
>>> residual = data_out - trend_out.predict(coordinates)
>>> print('{:.2f}'.format(residual[2, 2]))
500.00

Methods Summary

`Trend.filter`(coordinates, data[, weights])	Filter the data through the gridder and produce residuals.
`Trend.fit`(coordinates, data[, weights])	Fit the trend to the given data.
`Trend.get_params`([deep])	Get parameters for this estimator.
`Trend.grid`([region, shape, spacing, dims, …])	Interpolate the data onto a regular grid.
`Trend.jacobian`(coordinates[, dtype])	Make the Jacobian matrix for a 2D polynomial.
`Trend.predict`(coordinates)	Evaluate the polynomial trend on the given set of points.
`Trend.profile`(point1, point2, size[, dims, …])	Interpolate data along a profile between two points.
`Trend.scatter`([region, size, random_state, …])	Interpolate values onto a random scatter of points.
`Trend.score`(coordinates, data[, weights])	Score the gridder predictions against the given data.
`Trend.set_params`(**params)	Set the parameters of this estimator.

Trend.filter(coordinates, data, weights=None)¶

Filter the data through the gridder and produce residuals.

Calls fit on the data, evaluates the residuals (data - predicted data), and returns the coordinates, residuals, and weights.

No very useful by itself but this interface makes gridders compatible with other processing operations and is used by verde.Chain to join them together (for example, so you can fit a spline on the residuals of a trend).

Parameters

coordinates (tuple of arrays) – Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …).
data (array or tuple of arrays) – The data values of each data point. If the data has more than one component, data must be a tuple of arrays (one for each component).
weights (None or array or tuple of arrays) – If not None, then the weights assigned to each data point. If more than one data component is provided, you must provide a weights array for each data component (if not None).

Returns

coordinates, residuals, weights – The coordinates and weights are same as the input. Residuals are the input data minus the predicted data.

Trend.fit(coordinates, data, weights=None)[source]¶

Fit the trend to the given data.

The data region is captured and used as default for the grid and scatter methods.

All input arrays must have the same shape.

Parameters

coordinates (tuple of arrays) – Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). Only easting and northing will be used, all subsequent coordinates will be ignored.
data (array) – The data values of each data point.
weights (None or array) – If not None, then the weights assigned to each data point. Typically, this should be 1 over the data uncertainty squared.

Returns

self – Returns this estimator instance for chaining operations.

Trend.get_params(deep=True)¶

Get parameters for this estimator.

Parameters: deep (bool, default=True) – If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params (mapping of string to any) – Parameter names mapped to their values.

Trend.grid(region=None, shape=None, spacing=None, dims=None, data_names=None, projection=None, **kwargs)¶

Interpolate the data onto a regular grid.

The grid can be specified by either the number of points in each dimension (the shape) or by the grid node spacing. See verde.grid_coordinates for details. Other arguments for verde.grid_coordinates can be passed as extra keyword arguments (kwargs) to this method.

If the interpolator collected the input data region, then it will be used if region=None. Otherwise, you must specify the grid region.

Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output xarray.Dataset. Default names will be provided if none are given.

Parameters

region (list = [W, E, S, N]) – The boundaries of a given region in Cartesian or geographic coordinates.
shape (tuple = (n_north, n_east) or None) – The number of points in the South-North and West-East directions, respectively.
spacing (tuple = (s_north, s_east) or None) – The grid spacing in the South-North and West-East directions, respectively.
dims (list or None) – The names of the northing and easting data dimensions, respectively, in the output grid. Defaults to ['northing', 'easting']. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.
data_names (list of None) – The name(s) of the data variables in the output grid. Defaults to ['scalars'] for scalar data, ['east_component', 'north_component'] for 2D vector data, and ['east_component', 'north_component', 'vertical_component'] for 3D vector data.
projection (callable or None) – If not None, then should be a callable object projection(easting, northing) -> (proj_easting, proj_northing) that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated grid coordinates before passing them into predict. For example, you can use this to generate a geographic grid from a Cartesian gridder.

Returns

grid (xarray.Dataset) – The interpolated grid. Metadata about the interpolator is written to the attrs attribute.

See also

verde.grid_coordinates: Generate the coordinate values for the grid.

Trend.jacobian(coordinates, dtype='float64')[source]¶

Make the Jacobian matrix for a 2D polynomial.

Each column of the Jacobian is easting**i * northing**j for each (i, j) pair in the polynomial.

Parameters

coordinates (tuple of arrays) – Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). Only easting and northing will be used, all subsequent coordinates will be ignored.
dtype (str or numpy dtype) – The type of the output Jacobian numpy array.

Returns

jacobian (2D array) – The (n_data, n_coefficients) Jacobian matrix.

Examples

>>> import numpy as np
>>> east = np.linspace(0, 4, 5)
>>> north = np.linspace(-5, -1, 5)
>>> print(Trend(degree=1).jacobian((east, north), dtype=np.int))
[[ 1  0 -5]
 [ 1  1 -4]
 [ 1  2 -3]
 [ 1  3 -2]
 [ 1  4 -1]]
>>> print(Trend(degree=2).jacobian((east, north), dtype=np.int))
[[ 1  0 -5  0  0 25]
 [ 1  1 -4  1 -4 16]
 [ 1  2 -3  4 -6  9]
 [ 1  3 -2  9 -6  4]
 [ 1  4 -1 16 -4  1]]

Trend.predict(coordinates)[source]¶

Evaluate the polynomial trend on the given set of points.

Requires a fitted estimator (see fit).

Parameters: coordinates (tuple of arrays) – Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). Only easting and northing will be used, all subsequent coordinates will be ignored.
Returns: data (array) – The trend values evaluated on the given points.

Trend.profile(point1, point2, size, dims=None, data_names=None, projection=None, **kwargs)¶

Interpolate data along a profile between two points.

Generates the profile along a straight line assuming Cartesian distances. Point coordinates are generated by verde.profile_coordinates. Other arguments for this function can be passed as extra keyword arguments (kwargs) to this method.

Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output pandas.DataFrame. Default names are provided.

Includes the calculated Cartesian distance from point1 for each data point in the profile.

Parameters

point1 (tuple) – The easting and northing coordinates, respectively, of the first point.
point2 (tuple) – The easting and northing coordinates, respectively, of the second point.
size (int) – The number of points to generate.
dims (list or None) – The names of the northing and easting data dimensions, respectively, in the output dataframe. Defaults to ['northing', 'easting']. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.
data_names (list of None) – The name(s) of the data variables in the output dataframe. Defaults to ['scalars'] for scalar data, ['east_component', 'north_component'] for 2D vector data, and ['east_component', 'north_component', 'vertical_component'] for 3D vector data.
projection (callable or None) – If not None, then should be a callable object projection(easting, northing) -> (proj_easting, proj_northing) that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated profile coordinates before passing them into predict. For example, you can use this to generate a geographic profile from a Cartesian gridder.

Returns

table (pandas.DataFrame) – The interpolated values along the profile.

Trend.scatter(region=None, size=300, random_state=0, dims=None, data_names=None, projection=None, **kwargs)¶

Interpolate values onto a random scatter of points.

Point coordinates are generated by verde.scatter_points. Other arguments for this function can be passed as extra keyword arguments (kwargs) to this method.

If the interpolator collected the input data region, then it will be used if region=None. Otherwise, you must specify the grid region.

Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output pandas.DataFrame. Default names are provided.

Parameters

region (list = [W, E, S, N]) – The boundaries of a given region in Cartesian or geographic coordinates.
size (int) – The number of points to generate.
random_state (numpy.random.RandomState or an int seed) – A random number generator used to define the state of the random permutations. Use a fixed seed to make sure computations are reproducible. Use None to choose a seed automatically (resulting in different numbers with each run).
dims (list or None) – The names of the northing and easting data dimensions, respectively, in the output dataframe. Defaults to ['northing', 'easting']. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.
data_names (list of None) – The name(s) of the data variables in the output dataframe. Defaults to ['scalars'] for scalar data, ['east_component', 'north_component'] for 2D vector data, and ['east_component', 'north_component', 'vertical_component'] for 3D vector data.
projection (callable or None) – If not None, then should be a callable object projection(easting, northing) -> (proj_easting, proj_northing) that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated scatter coordinates before passing them into predict. For example, you can use this to generate a geographic scatter from a Cartesian gridder.

Returns

table (pandas.DataFrame) – The interpolated values on a random set of points.

Trend.score(coordinates, data, weights=None)¶

Score the gridder predictions against the given data.

Calculates the R^2 coefficient of determination of between the predicted values and the given data values. A maximum score of 1 means a perfect fit. The score can be negative.

If the data has more than 1 component, the scores of each component will be averaged.

Parameters

coordinates (tuple of arrays) – Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …).
data (array or tuple of arrays) – The data values of each data point. If the data has more than one component, data must be a tuple of arrays (one for each component).
weights (None or array or tuple of arrays) – If not None, then the weights assigned to each data point. If more than one data component is provided, you must provide a weights array for each data component (if not None).

Returns

score (float) – The R^2 score

Trend.set_params(**params)¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters: **params (dict) – Estimator parameters.
Returns: self (object) – Estimator instance.