Note
Click here to download the full example code
Gridding 2D vectors (uncoupled)¶
We can use verde.Vector to simultaneously process and grid all
components of vector data. Each component is processed and gridded separately (see
verde.VectorSpline2D for a coupled alternative) but we have the convenience of
dealing with a single estimator. verde.Vector can be combined with
verde.Trend, verde.Spline, and verde.Chain to create a full
processing pipeline.
Out:
station_id ... wind_speed_north_knots
0 0F2 ... -2.357185
1 11R ... 2.982564
2 2F5 ... -0.311412
3 3T5 ... 3.018448
4 5C1 ... 1.090743
[5 rows x 6 columns]
Chain(steps=[('mean', BlockReduce(adjust='spacing', center_coordinates=False,
reduction=<function mean at 0x1532bbad1378>, region=None,
spacing=37000.0)), ('trend', Vector(components=[Trend(degree=1), Trend(degree=1)])), ('spline', Vector(components=[Spline(damping=1e-10, engine='auto', force_coords=None, mindist=500000.0), Spline(damping=1e-10, engine='auto', force_coords=None, mindist=500000.0)]))])
Cross-validation R^2 score: 0.78
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import numpy as np
import pyproj
import verde as vd
# Fetch the wind speed data from Texas.
data = vd.datasets.fetch_texas_wind()
print(data.head())
# Separate out some of the data into utility variables
coordinates = (data.longitude.values, data.latitude.values)
region = vd.get_region(coordinates)
# Use a Mercator projection because Spline is a Cartesian gridder
projection = pyproj.Proj(proj="merc", lat_ts=data.latitude.mean())
# Split the data into a training and testing set. We'll fit the gridder on the training
# set and use the testing set to evaluate how well the gridder is performing.
train, test = vd.train_test_split(
projection(*coordinates),
(data.wind_speed_east_knots, data.wind_speed_north_knots),
random_state=2,
)
# We'll make a 20 arc-minute grid
spacing = 20 / 60
# Chain together a blocked mean to avoid aliasing, a polynomial trend (Spline usually
# requires de-trended data), and finally a Spline for each component. Notice that
# BlockReduce can work on multicomponent data without the use of Vector.
chain = vd.Chain(
[
("mean", vd.BlockReduce(np.mean, spacing * 111e3)),
("trend", vd.Vector([vd.Trend(degree=1) for i in range(2)])),
(
"spline",
vd.Vector([vd.Spline(damping=1e-10, mindist=500e3) for i in range(2)]),
),
]
)
print(chain)
# Fit on the training data
chain.fit(*train)
# And score on the testing data. The best possible score is 1, meaning a perfect
# prediction of the test data.
score = chain.score(*test)
print("Cross-validation R^2 score: {:.2f}".format(score))
# Interpolate the wind speed onto a regular geographic grid and mask the data that are
# far from the observation points
grid_full = chain.grid(
region, spacing=spacing, projection=projection, dims=["latitude", "longitude"]
)
grid = vd.distance_mask(
coordinates, maxdist=3 * spacing * 111e3, grid=grid_full, projection=projection
)
# Make maps of the original and gridded wind speed
plt.figure(figsize=(6, 6))
ax = plt.axes(projection=ccrs.Mercator())
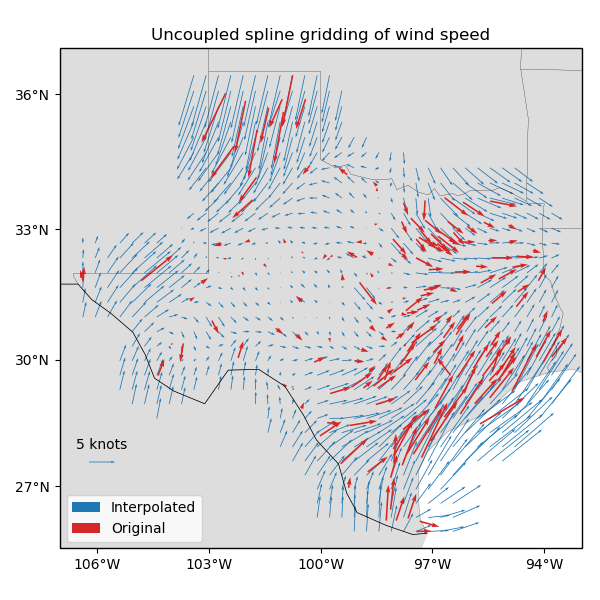
ax.set_title("Uncoupled spline gridding of wind speed")
tmp = ax.quiver(
grid.longitude.values,
grid.latitude.values,
grid.east_component.values,
grid.north_component.values,
width=0.0015,
scale=100,
color="tab:blue",
transform=ccrs.PlateCarree(),
label="Interpolated",
)
ax.quiver(
*coordinates,
data.wind_speed_east_knots.values,
data.wind_speed_north_knots.values,
width=0.003,
scale=100,
color="tab:red",
transform=ccrs.PlateCarree(),
label="Original",
)
ax.quiverkey(tmp, 0.17, 0.23, 5, label="5 knots", coordinates="figure")
ax.legend(loc="lower left")
# Use an utility function to add tick labels and land and ocean features to the map.
vd.datasets.setup_texas_wind_map(ax)
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 0.627 seconds)