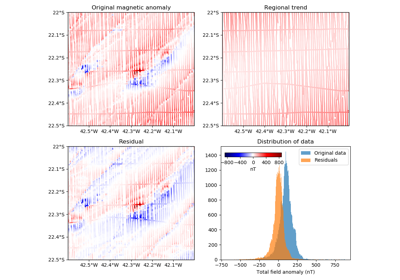
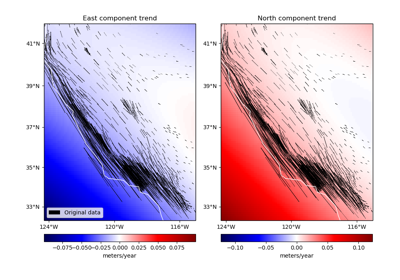
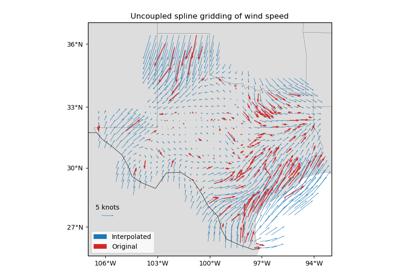
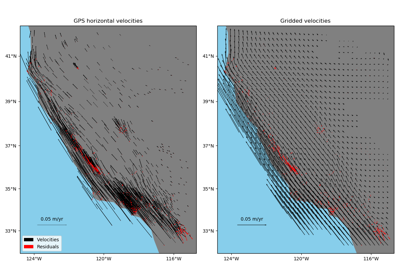
verde.Trend¶
-
class
verde.Trend(degree)[source]¶ Fit a 2D polynomial trend to spatial data.
The trend is estimated through weighted least-squares regression.
The Jacobian (design, sensitivity, feature, etc) matrix for the regression is normalized using
sklearn.preprocessing.StandardScalerwithout centering the mean so that the transformation can be undone in the estimated coefficients.Parameters: - degree : int
The degree of the polynomial. Must be >= 1.
Examples
>>> from verde import grid_coordinates >>> coordinates = grid_coordinates((1, 5, -5, -1), shape=(5, 5)) >>> data = 10 + 2*coordinates[0] - 0.4*coordinates[1] >>> trend = Trend(degree=1).fit(coordinates, data) >>> print(', '.join(['{:.1f}'.format(i) for i in trend.coef_])) 10.0, 2.0, -0.4 >>> import numpy as np >>> np.allclose(trend.predict(coordinates), data) True >>> # Use weights to account for outliers >>> data_out = data.copy() >>> data_out[2, 2] += 500 >>> weights = np.ones_like(data) >>> weights[2, 2] = 1e-10 >>> trend_out = Trend(degree=1).fit(coordinates, data_out, weights) >>> print(', '.join(['{:.1f}'.format(i) for i in trend_out.coef_])) 10.0, 2.0, -0.4 >>> residual = data_out - trend_out.predict(coordinates) >>> print('{:.2f}'.format(residual[2, 2])) 500.00
Attributes: Methods
filter(coordinates, data[, weights])Filter the data through the gridder and produce residuals. fit(coordinates, data[, weights])Fit the trend to the given data. get_params([deep])Get parameters for this estimator. grid([region, shape, spacing, dims, …])Interpolate the data onto a regular grid. jacobian(coordinates[, dtype])Make the Jacobian matrix for a 2D polynomial. predict(coordinates)Evaluate the polynomial trend on the given set of points. profile(point1, point2, size[, dims, …])Interpolate data along a profile between two points. scatter([region, size, random_state, dims, …])Interpolate values onto a random scatter of points. score(coordinates, data[, weights])Score the gridder predictions against the given data. set_params(**params)Set the parameters of this estimator.
Examples using verde.Trend¶
-
Trend.filter(coordinates, data, weights=None)¶ Filter the data through the gridder and produce residuals.
Calls
fiton the data, evaluates the residuals (data - predicted data), and returns the coordinates, residuals, and weights.No very useful by itself but this interface makes gridders compatible with other processing operations and is used by
verde.Chainto join them together (for example, so you can fit a spline on the residuals of a trend).Parameters: - coordinates : tuple of arrays
Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …).
- data : array or tuple of arrays
The data values of each data point. If the data has more than one component, data must be a tuple of arrays (one for each component).
- weights : None or array or tuple of arrays
If not None, then the weights assigned to each data point. If more than one data component is provided, you must provide a weights array for each data component (if not None).
Returns: - coordinates, residuals, weights
The coordinates and weights are same as the input. Residuals are the input data minus the predicted data.
-
Trend.fit(coordinates, data, weights=None)[source]¶ Fit the trend to the given data.
The data region is captured and used as default for the
gridandscattermethods.All input arrays must have the same shape.
Parameters: - coordinates : tuple of arrays
Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). Only easting and northing will be used, all subsequent coordinates will be ignored.
- data : array
The data values of each data point.
- weights : None or array
If not None, then the weights assigned to each data point. Typically, this should be 1 over the data uncertainty squared.
Returns: - self
Returns this estimator instance for chaining operations.
-
Trend.get_params(deep=True)¶ Get parameters for this estimator.
Parameters: - deep : boolean, optional
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: - params : mapping of string to any
Parameter names mapped to their values.
-
Trend.grid(region=None, shape=None, spacing=None, dims=None, data_names=None, projection=None, **kwargs)¶ Interpolate the data onto a regular grid.
The grid can be specified by either the number of points in each dimension (the shape) or by the grid node spacing. See
verde.grid_coordinatesfor details. Other arguments forverde.grid_coordinatescan be passed as extra keyword arguments (kwargs) to this method.If the interpolator collected the input data region, then it will be used if
region=None. Otherwise, you must specify the grid region.Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output
xarray.Dataset. Default names will be provided if none are given.Parameters: - region : list = [W, E, S, N]
The boundaries of a given region in Cartesian or geographic coordinates.
- shape : tuple = (n_north, n_east) or None
The number of points in the South-North and West-East directions, respectively.
- spacing : tuple = (s_north, s_east) or None
The grid spacing in the South-North and West-East directions, respectively.
- dims : list or None
The names of the northing and easting data dimensions, respectively, in the output grid. Defaults to
['northing', 'easting']. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.- data_names : list of None
The name(s) of the data variables in the output grid. Defaults to
['scalars']for scalar data,['east_component', 'north_component']for 2D vector data, and['east_component', 'north_component', 'vertical_component']for 3D vector data.- projection : callable or None
If not None, then should be a callable object
projection(easting, northing) -> (proj_easting, proj_northing)that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated grid coordinates before passing them intopredict. For example, you can use this to generate a geographic grid from a Cartesian gridder.
Returns: - grid : xarray.Dataset
The interpolated grid. Metadata about the interpolator is written to the
attrsattribute.
See also
verde.grid_coordinates- Generate the coordinate values for the grid.
-
Trend.jacobian(coordinates, dtype='float64')[source]¶ Make the Jacobian matrix for a 2D polynomial.
Each column of the Jacobian is
easting**i * northing**jfor each (i, j) pair in the polynomial.Parameters: - coordinates : tuple of arrays
Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). Only easting and northing will be used, all subsequent coordinates will be ignored.
- dtype : str or numpy dtype
The type of the output Jacobian numpy array.
Returns: - jacobian : 2D array
The (n_data, n_coefficients) Jacobian matrix.
Examples
>>> import numpy as np >>> east = np.linspace(0, 4, 5) >>> north = np.linspace(-5, -1, 5) >>> print(Trend(degree=1).jacobian((east, north), dtype=np.int)) [[ 1 0 -5] [ 1 1 -4] [ 1 2 -3] [ 1 3 -2] [ 1 4 -1]] >>> print(Trend(degree=2).jacobian((east, north), dtype=np.int)) [[ 1 0 -5 0 0 25] [ 1 1 -4 1 -4 16] [ 1 2 -3 4 -6 9] [ 1 3 -2 9 -6 4] [ 1 4 -1 16 -4 1]]
-
Trend.predict(coordinates)[source]¶ Evaluate the polynomial trend on the given set of points.
Requires a fitted estimator (see
fit).Parameters: - coordinates : tuple of arrays
Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …). Only easting and northing will be used, all subsequent coordinates will be ignored.
Returns: - data : array
The trend values evaluated on the given points.
-
Trend.profile(point1, point2, size, dims=None, data_names=None, projection=None, **kwargs)¶ Interpolate data along a profile between two points.
Generates the profile along a straight line assuming Cartesian distances. Point coordinates are generated by
verde.profile_coordinates. Other arguments for this function can be passed as extra keyword arguments (kwargs) to this method.Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output
pandas.DataFrame. Default names are provided.Includes the calculated Cartesian distance from point1 for each data point in the profile.
Parameters: - point1 : tuple
The easting and northing coordinates, respectively, of the first point.
- point2 : tuple
The easting and northing coordinates, respectively, of the second point.
- size : int
The number of points to generate.
- dims : list or None
The names of the northing and easting data dimensions, respectively, in the output dataframe. Defaults to
['northing', 'easting']. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.- data_names : list of None
The name(s) of the data variables in the output dataframe. Defaults to
['scalars']for scalar data,['east_component', 'north_component']for 2D vector data, and['east_component', 'north_component', 'vertical_component']for 3D vector data.- projection : callable or None
If not None, then should be a callable object
projection(easting, northing) -> (proj_easting, proj_northing)that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated profile coordinates before passing them intopredict. For example, you can use this to generate a geographic profile from a Cartesian gridder.
Returns: - table : pandas.DataFrame
The interpolated values along the profile.
-
Trend.scatter(region=None, size=300, random_state=0, dims=None, data_names=None, projection=None, **kwargs)¶ Interpolate values onto a random scatter of points.
Point coordinates are generated by
verde.scatter_points. Other arguments for this function can be passed as extra keyword arguments (kwargs) to this method.If the interpolator collected the input data region, then it will be used if
region=None. Otherwise, you must specify the grid region.Use the dims and data_names arguments to set custom names for the dimensions and the data field(s) in the output
pandas.DataFrame. Default names are provided.Parameters: - region : list = [W, E, S, N]
The boundaries of a given region in Cartesian or geographic coordinates.
- size : int
The number of points to generate.
- random_state : numpy.random.RandomState or an int seed
A random number generator used to define the state of the random permutations. Use a fixed seed to make sure computations are reproducible. Use
Noneto choose a seed automatically (resulting in different numbers with each run).- dims : list or None
The names of the northing and easting data dimensions, respectively, in the output dataframe. Defaults to
['northing', 'easting']. NOTE: This is an exception to the “easting” then “northing” pattern but is required for compatibility with xarray.- data_names : list of None
The name(s) of the data variables in the output dataframe. Defaults to
['scalars']for scalar data,['east_component', 'north_component']for 2D vector data, and['east_component', 'north_component', 'vertical_component']for 3D vector data.- projection : callable or None
If not None, then should be a callable object
projection(easting, northing) -> (proj_easting, proj_northing)that takes in easting and northing coordinate arrays and returns projected northing and easting coordinate arrays. This function will be used to project the generated scatter coordinates before passing them intopredict. For example, you can use this to generate a geographic scatter from a Cartesian gridder.
Returns: - table : pandas.DataFrame
The interpolated values on a random set of points.
-
Trend.score(coordinates, data, weights=None)¶ Score the gridder predictions against the given data.
Calculates the R^2 coefficient of determination of between the predicted values and the given data values. A maximum score of 1 means a perfect fit. The score can be negative.
If the data has more than 1 component, the scores of each component will be averaged.
Parameters: - coordinates : tuple of arrays
Arrays with the coordinates of each data point. Should be in the following order: (easting, northing, vertical, …).
- data : array or tuple of arrays
The data values of each data point. If the data has more than one component, data must be a tuple of arrays (one for each component).
- weights : None or array or tuple of arrays
If not None, then the weights assigned to each data point. If more than one data component is provided, you must provide a weights array for each data component (if not None).
Returns: - score : float
The R^2 score
-
Trend.set_params(**params)¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.Returns: - self