Note
Click here to download the full example code
Overview¶
Verde provides classes and functions for processing spatial data, like bathymetry, GPS, temperature, gravity, or anything else that is measured along a surface. The main focus is on methods for gridding such data (interpolating on a regular grid). You’ll also find other analysis methods that are often used in combination with gridding, like trend removal and blocked operations.
Conventions¶
Before we get started, here are a few of the conventions we use across Verde:
Coordinates can be Cartesian or Geographic. We generally make no assumptions about which one you’re using.
All functions and classes expect coordinates in the order: West-East and South-North. This applies to the actual coordinate values, bounding regions, grid spacing, etc. Exceptions to this rule are the
dimsandshapearguments.We don’t use names like “x” and “y” to avoid ambiguity. Cartesian coordinates are “easting” and “northing” and Geographic coordinates are “longitude” and “latitude”.
The term “region” means the bounding box of the data. It is ordered west, east, south, north.
The library¶
Most classes and functions are available through the verde top level package.
The only exceptions are the functions related to loading sample data, which are in
verde.datasets. Throughout the documentation we’ll use vd as the alias for
verde.
import verde as vd
The gridder interface¶
All gridding and trend estimation classes in Verde share the same interface (they all
inherit from verde.base.BaseGridder). Since most gridders in Verde are linear
models, we based our gridder interface on the scikit-learn estimator interface: they all implement a
fit method that estimates the model parameters based
on data and a predict method that calculates new data
based on the estimated parameters.
Unlike scikit-learn, our data model is not a feature matrix and a target vector (e.g.,
est.fit(X, y)) but a tuple of coordinate arrays and a data vector (e.g.,
grd.fit((easting, northing), data)). This makes more sense for spatial data and is
common to all classes and functions in Verde.
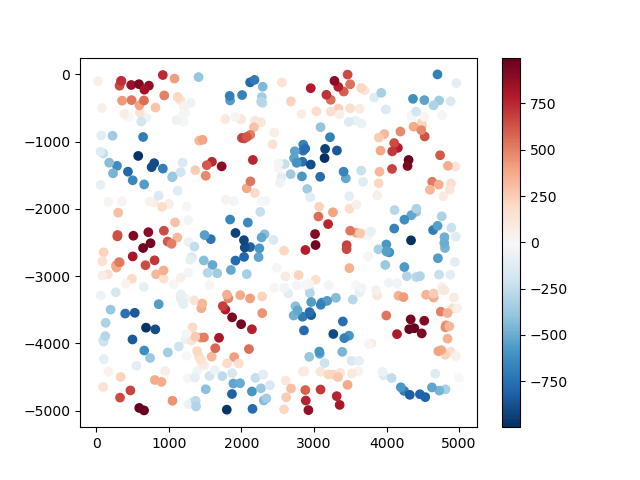
As an example, let’s generate some synthetic data using
verde.datasets.CheckerBoard:
data = vd.datasets.CheckerBoard().scatter(size=500, random_state=0)
print(data.head())
Out:
northing easting scalars
0 -3448.095870 2744.067520 -417.745960
1 -3134.825681 3575.946832 -10.460197
2 -2375.147789 3013.816880 914.277006
3 -1247.024885 2724.415915 -534.571829
4 -3332.462671 2118.273997 407.865799
The data are random points taken from a checkerboard function and returned to us in a
pandas.DataFrame:
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(data.easting, data.northing, c=data.scalars, cmap="RdBu_r")
plt.colorbar()
plt.show()
Now we can use the bi-harmonic spline method [Sandwell1987] to fit this data. First,
we create a new verde.Spline:
Out:
Spline()
Before we can use the spline, we need to fit it to our synthetic data. After that, we can use the spline to predict values anywhere:
spline.fit((data.easting, data.northing), data.scalars)
# Generate coordinates for a regular grid with 100 m grid spacing (assuming coordinates
# are in meters).
grid_coords = vd.grid_coordinates(region=(0, 5000, -5000, 0), spacing=100)
gridded_scalars = spline.predict(grid_coords)
plt.figure()
plt.pcolormesh(grid_coords[0], grid_coords[1], gridded_scalars, cmap="RdBu_r")
plt.colorbar()
plt.show()
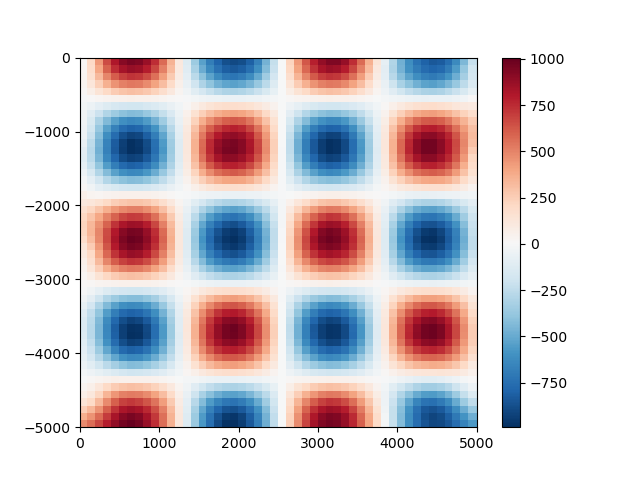
We can compare our predictions with the true values for the checkerboard function
using the score method to calculate the R² coefficient of
determination.
true_values = vd.datasets.CheckerBoard().predict(grid_coords)
print(spline.score(grid_coords, true_values))
Out:
0.9950450871662229
Generating grids and profiles¶
A more convenient way of generating grids is through the
grid method. It will automatically generate
coordinates and output an xarray.Dataset.
grid = spline.grid(spacing=30)
print(grid)
Out:
<xarray.Dataset>
Dimensions: (easting: 167, northing: 168)
Coordinates:
* easting (easting) float64 23.48 53.42 83.37 ... 4.964e+03 4.994e+03
* northing (northing) float64 -4.997e+03 -4.967e+03 ... -30.88 -0.9571
Data variables:
scalars (northing, easting) float64 495.6 521.3 549.0 ... -184.7 -139.6
Attributes:
metadata: Generated by Spline()
grid uses default names for the coordinates (“easting”
and “northing”) and data variables (“scalars”). You can overwrite these names by
setting the dims and data_names arguments.
grid = spline.grid(spacing=30, dims=["latitude", "longitude"], data_names=["gravity"])
print(grid)
plt.figure()
grid.gravity.plot.pcolormesh()
plt.show()
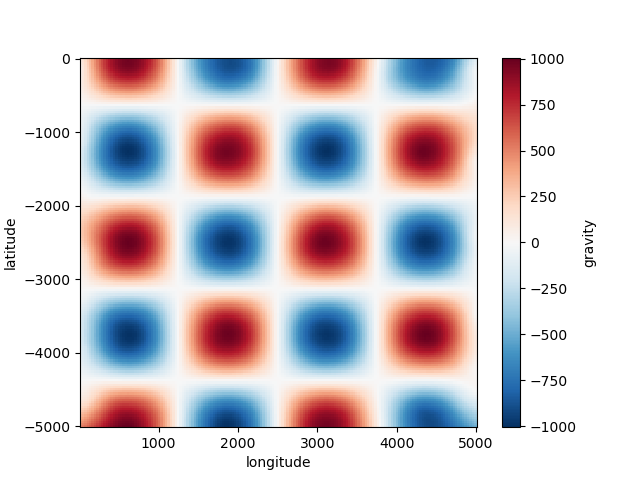
Out:
<xarray.Dataset>
Dimensions: (latitude: 168, longitude: 167)
Coordinates:
* longitude (longitude) float64 23.48 53.42 83.37 ... 4.964e+03 4.994e+03
* latitude (latitude) float64 -4.997e+03 -4.967e+03 ... -30.88 -0.9571
Data variables:
gravity (latitude, longitude) float64 495.6 521.3 549.0 ... -184.7 -139.6
Attributes:
metadata: Generated by Spline()
Gridders can also be used to interpolate data on a straight line between two points
using the profile method. The profile data are
returned as a pandas.DataFrame.
prof = spline.profile(point1=(0, 0), point2=(5000, -5000), size=200)
print(prof.head())
plt.figure()
plt.plot(prof.distance, prof.scalars, "-")
plt.show()
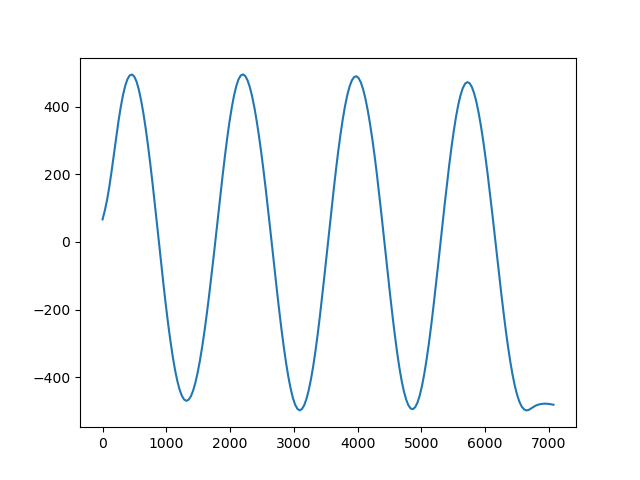
Out:
northing easting distance scalars
0 0.000000 0.000000 0.000000 66.785376
1 -25.125628 25.125628 35.533004 92.895113
2 -50.251256 50.251256 71.066008 124.644012
3 -75.376884 75.376884 106.599012 163.870392
4 -100.502513 100.502513 142.132016 209.836541
Wrap up¶
This covers the basics of using Verde. Most use cases and examples in the documentation will involve some variation of the following workflow:
Load data (coordinates and data values)
Create a gridder
Fit the gridder to the data
Total running time of the script: ( 0 minutes 1.514 seconds)