Grid Coordinates

Creating the coordinates for regular grids in Verde is done using the verde.grid_coordinates function. It creates a set of regularly spaced points in both the west-east and south-north directions, i.e. a two-dimensional spatial grid. These points are then used by the Verde gridders to interpolate between data points. As such, all .grid methods (like verde.Spline.grid) take as input the configuration parameters for verde.grid_coordinates. The grid can be specified either by the number of points in each dimension (the shape) or by the grid node spacing.

import numpy as np
import matplotlib.pyplot as plt
import verde as vd
from matplotlib.patches import Rectangle

First let’s create a region that is 1000 units west-east and 1000 units south-north, and we will set an initial spacing to 100 units.

spacing = 100
west, east, south, north = 0, 1000, 0, 1000
region = (west, east, south, north)

# create the grid coordinates
easting, northing = vd.grid_coordinates(region=region, spacing=spacing)

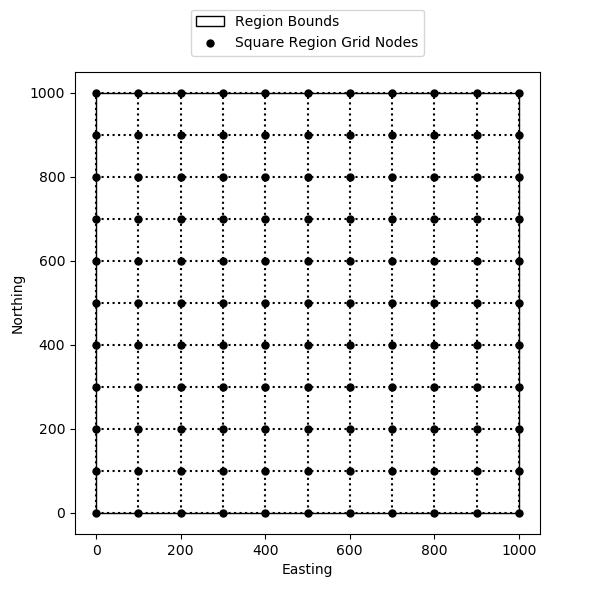
We can check the dimensions of the grid coordinates. The region is 1000 units and the spacing is 100 units, so the shape of the segments is 10x10. However, the number of grid nodes in this case is one more than the number of segments. So our grid coordinates have a shape of 11x11.

print(easting.shape, northing.shape)

Out:

(11, 11) (11, 11)

Let’s define two functions to visualize the region bounds and grid points

def plot_region(ax, region):
    "Plot the region as a solid line."
    west, east, south, north = region
    ax.add_patch(
        plt.Rectangle((west, south), east, north, fill=None, label="Region Bounds")
    )


def plot_grid(ax, coordinates, linestyles="dotted", region=None, pad=50, **kwargs):
    "Plot the grid coordinates as dots and lines."
    data_region = vd.get_region(coordinates)
    ax.vlines(
        coordinates[0][0],
        ymin=data_region[2],
        ymax=data_region[3],
        linestyles=linestyles,
        zorder=0,
    )
    ax.hlines(
        coordinates[1][:, 1],
        xmin=data_region[0],
        xmax=data_region[1],
        linestyles=linestyles,
        zorder=0,
    )
    ax.scatter(*coordinates, **kwargs)
    if pad:
        padded = vd.pad_region(region, pad=pad)
        plt.xlim(padded[:2])
        plt.ylim(padded[2:])

Visualize our region and grid coordinates using our functions

plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
plot_region(ax=ax, region=region)
plot_grid(
    ax=ax,
    coordinates=(easting, northing),
    region=region,
    label="Square Region Grid Nodes",
    marker=".",
    color="black",
    s=100,
)

plt.xlabel("Easting")
plt.ylabel("Northing")
plt.legend(loc="upper center", bbox_to_anchor=(0.5, 1.15))
plt.show()

Out:

/home/leo/src/verde/tutorials/grid_coordinates.py:96: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()

Adjusting region boundaries when creating the grid coordinates

Now let’s change our spacing to 300 units. Because the range of the west-east and south-north boundaries are not multiples of 300, we must choose to change either:

• the boundaries of the region in order to fit the spacing, or

• the spacing in order to fit the region boundaries.

We could tell verde.grid_coordinates to adjust the region boundaries by passing adjust="region".

spacing = 300
region_easting, region_northing = vd.grid_coordinates(
    region=region, spacing=spacing, adjust="region"
)
print(region_easting.shape, region_northing.shape)

Out:

(4, 4) (4, 4)

With the spacing set at 300 units and a 4 by 4 grid of regular dimensions, verde.grid_coordinates calculates the spatial location of each grid point and adjusts the region so that the maximum northing and maximum easting values are divisible by the spacing. In this example, both the easting and northing have 3 segments (4 nodes) that are each 300 units long, meaning the easting and northing span from 0 to 900. Both dimensions are divisible by 300.

print(region_easting)
print(region_northing)

Out:

[[  0. 300. 600. 900.]
 [  0. 300. 600. 900.]
 [  0. 300. 600. 900.]
 [  0. 300. 600. 900.]]
[[  0.   0.   0.   0.]
 [300. 300. 300. 300.]
 [600. 600. 600. 600.]
 [900. 900. 900. 900.]]

By default, if adjust is not assigned to "region" or "spacing", then verde.grid_coordinates will adjust the spacing. With the adjust parameter set to spacing verde.grid_coordinates creates grid nodes in a similar manner as when it adjusts the region. However, it doesn’t readjust the region so that it is divisble by the spacing before creating the grid. This means the grid will have the same number of grid points no matter if the adjust parameter is set to region or spacing.

Adjusting spacing when creating the grid

Now let’s adjust the spacing of the grid points by passing adjust="spacing" to verde.grid_coordinates.

spacing_easting, spacing_northing = vd.grid_coordinates(
    region=region, spacing=spacing, adjust="spacing"
)
print(spacing_easting.shape, spacing_northing.shape)

Out:

(4, 4) (4, 4)

However the regular spacing between the grid points is no longer 300 units.

print(spacing_easting)
print(spacing_northing)

Out:

[[   0.          333.33333333  666.66666667 1000.        ]
 [   0.          333.33333333  666.66666667 1000.        ]
 [   0.          333.33333333  666.66666667 1000.        ]
 [   0.          333.33333333  666.66666667 1000.        ]]
[[   0.            0.            0.            0.        ]
 [ 333.33333333  333.33333333  333.33333333  333.33333333]
 [ 666.66666667  666.66666667  666.66666667  666.66666667]
 [1000.         1000.         1000.         1000.        ]]

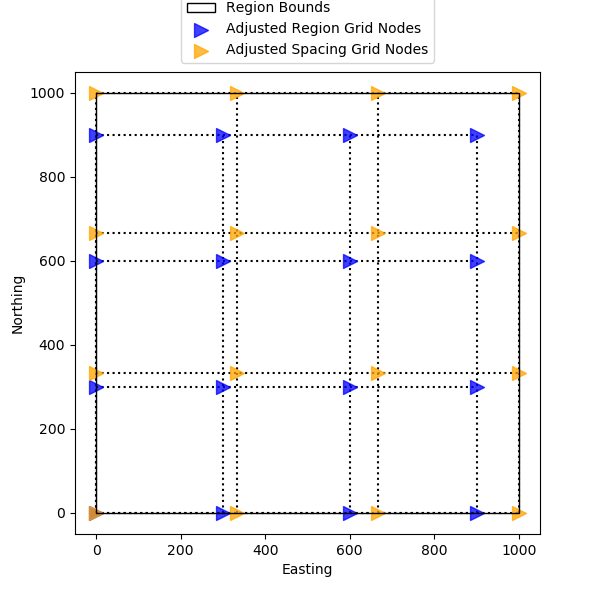
Visualize the different adjustments

Let’s visualize the difference between the original region bounds, the adjusted region grid nodes, and the adjusted spacing grid nodes. Note the adjusted spacing grid nodes keep the original region, while the adjusted region grid nodes on the north and east side of the region have moved.

plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
plot_region(ax=ax, region=region)
plot_grid(
    ax=ax,
    coordinates=(region_easting, region_northing),
    region=region,
    label="Adjusted Region Grid Nodes",
    marker=">",
    color="blue",
    alpha=0.75,
    s=100,
)
plot_grid(
    ax=ax,
    coordinates=(spacing_easting, spacing_northing),
    region=region,
    label="Adjusted Spacing Grid Nodes",
    marker=">",
    color="orange",
    alpha=0.75,
    s=100,
)
plt.xlabel("Easting")
plt.ylabel("Northing")
plt.legend(loc="upper center", bbox_to_anchor=(0.5, 1.18))
plt.show()

Out:

/home/leo/src/verde/tutorials/grid_coordinates.py:191: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()

Pixel Registration

Pixel registration locates the grid points in the middle of the grid segments rather than in the corner of each grid node.

First, let’s take our 1000x1000 region and use the 100 unit spacing from the first example and set the pixel_register parameter to True. Without pixel registration our grid should have dimensions of 11x11. With pixel registration we expect the dimensions of the grid to be the dimensions of the non-registered grid minus one, or equal to the number of segments between the grid points in the non-registered grid (10x10).

spacing = 100
pixel_easting, pixel_northing = vd.grid_coordinates(
    region=region, spacing=spacing, pixel_register=True
)
print(pixel_easting.shape, pixel_northing.shape)

Out:

(10, 10) (10, 10)

And we can check the coordinates for the grid points with pixel registration.

print(pixel_easting)
print(pixel_northing)

Out:

[[ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]
 [ 50. 150. 250. 350. 450. 550. 650. 750. 850. 950.]]
[[ 50.  50.  50.  50.  50.  50.  50.  50.  50.  50.]
 [150. 150. 150. 150. 150. 150. 150. 150. 150. 150.]
 [250. 250. 250. 250. 250. 250. 250. 250. 250. 250.]
 [350. 350. 350. 350. 350. 350. 350. 350. 350. 350.]
 [450. 450. 450. 450. 450. 450. 450. 450. 450. 450.]
 [550. 550. 550. 550. 550. 550. 550. 550. 550. 550.]
 [650. 650. 650. 650. 650. 650. 650. 650. 650. 650.]
 [750. 750. 750. 750. 750. 750. 750. 750. 750. 750.]
 [850. 850. 850. 850. 850. 850. 850. 850. 850. 850.]
 [950. 950. 950. 950. 950. 950. 950. 950. 950. 950.]]

If we set pixel_register to False the function will return the grid coordinates of the nodes instead of pixel centers, resulting in an extra point in each direction.

easting, northing = vd.grid_coordinates(
    region=region, spacing=spacing, pixel_register=False
)
print(easting.shape, northing.shape)

Out:

(11, 11) (11, 11)

Again we can check the coordinates for grid points with spacing adjustment.

print(easting)
print(northing)

Out:

[[   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]
 [   0.  100.  200.  300.  400.  500.  600.  700.  800.  900. 1000.]]
[[   0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.]
 [ 100.  100.  100.  100.  100.  100.  100.  100.  100.  100.  100.]
 [ 200.  200.  200.  200.  200.  200.  200.  200.  200.  200.  200.]
 [ 300.  300.  300.  300.  300.  300.  300.  300.  300.  300.  300.]
 [ 400.  400.  400.  400.  400.  400.  400.  400.  400.  400.  400.]
 [ 500.  500.  500.  500.  500.  500.  500.  500.  500.  500.  500.]
 [ 600.  600.  600.  600.  600.  600.  600.  600.  600.  600.  600.]
 [ 700.  700.  700.  700.  700.  700.  700.  700.  700.  700.  700.]
 [ 800.  800.  800.  800.  800.  800.  800.  800.  800.  800.  800.]
 [ 900.  900.  900.  900.  900.  900.  900.  900.  900.  900.  900.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]]

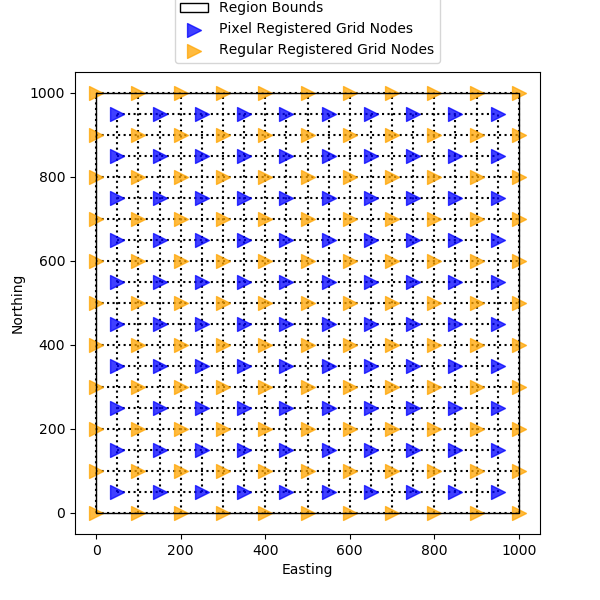
Lastly, we can visualize the pixel-registered grid points to see where they fall within the original region bounds.

plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
plot_region(ax=ax, region=region)
plot_grid(
    ax=ax,
    coordinates=(pixel_easting, pixel_northing),
    region=region,
    label="Pixel Registered Grid Nodes",
    marker=">",
    color="blue",
    alpha=0.75,
    s=100,
)
plot_grid(
    ax=ax,
    coordinates=(easting, northing),
    region=region,
    label="Regular Registered Grid Nodes",
    marker=">",
    color="orange",
    alpha=0.75,
    s=100,
)

plt.xlabel("Easting")
plt.ylabel("Northing")
plt.legend(loc="upper center", bbox_to_anchor=(0.5, 1.18))
plt.show()

Out:

/home/leo/src/verde/tutorials/grid_coordinates.py:265: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()

Extra Coordinates

In some cases, you might need an additional coordinate such as a height or a time that is associated with your coordinate grid. The extra_coords parameter in verde.grid_coordinates creates an extra coordinate array that is the same shape as the coordinate grid, but contains a constant value. For example, let’s add a constant height of 1000 units and time of 1 to our coordinate grid.

easting, northing, height, time = vd.grid_coordinates(
    region=region, spacing=spacing, extra_coords=[1000, 1]
)

print(easting.shape, northing.shape, height.shape, time.shape)

Out:

(11, 11) (11, 11) (11, 11) (11, 11)

And we can print the height array to verify that it is correct

print(height)

Out:

[[1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]
 [1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.]]

And we can print the time array as well

print(time)

Out:

[[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]