Normal gravity
Contents
Normal gravity#
One of the main uses for ellipsoids in geodesy and geophysics is the computation of normal gravity (usually represented by \(\gamma\)). The exact calculation and underlying assumptions are a bit different between the different types of ellipsoids.
Oblate ellipsoids#
Method boule.Ellipsoid.normal_gravity performs the normal gravity
calculations.
It can operate on single values:
import boule as bl
gamma = bl.WGS84.normal_gravity(latitude=45, height=50)
print(f"{gamma:.2f} mGal")
980604.35 mGal
Or on numpy array-like data (including pandas.DataFrame and
xarray.DataArray):
import numpy as np
height = np.linspace(0, 1000, 10)
gamma = bl.WGS84.normal_gravity(latitude=45, height=height)
print(gamma)
[980619.77693773 980585.4934137 980551.21168079 980516.93173896
980482.65358805 980448.3772279 980414.10265843 980379.82987947
980345.55889092 980311.28969268]
The arrays can be multi-dimensional so we can use verde to generate a
grid of normal gravity:
import verde as vd
longitude, latitude = vd.grid_coordinates(
region=[0, 360, -90, 90], spacing=0.5,
)
gamma = bl.WGS84.normal_gravity(latitude=latitude, height=10_000)
print(gamma)
[[980142.33509235 980142.33509235 980142.33509235 ... 980142.33509235
980142.33509235 980142.33509235]
[980141.93808117 980141.93808117 980141.93808117 ... 980141.93808117
980141.93808117 980141.93808117]
[980140.7471697 980140.7471697 980140.7471697 ... 980140.7471697
980140.7471697 980140.7471697 ]
...
[980140.7471697 980140.7471697 980140.7471697 ... 980140.7471697
980140.7471697 980140.7471697 ]
[980141.93808117 980141.93808117 980141.93808117 ... 980141.93808117
980141.93808117 980141.93808117]
[980142.33509235 980142.33509235 980142.33509235 ... 980142.33509235
980142.33509235 980142.33509235]]
Which can be put in a xarray.Dataset:
grid = vd.make_xarray_grid(
(longitude, latitude), gamma, data_names="normal_gravity",
)
grid
<xarray.Dataset>
Dimensions: (northing: 361, easting: 721)
Coordinates:
* easting (easting) float64 0.0 0.5 1.0 1.5 ... 359.0 359.5 360.0
* northing (northing) float64 -90.0 -89.5 -89.0 ... 89.0 89.5 90.0
Data variables:
normal_gravity (northing, easting) float64 9.801e+05 ... 9.801e+05And plotted with pygmt:
import pygmt
fig = pygmt.Figure()
fig.grdimage(grid.normal_gravity, projection="W20c", cmap="viridis")
fig.basemap(frame=["af", "WEsn"])
fig.colorbar(position="JCB+w10c", frame=["af", 'y+l"mGal"', 'x+l"WGS84"'])
fig.show()
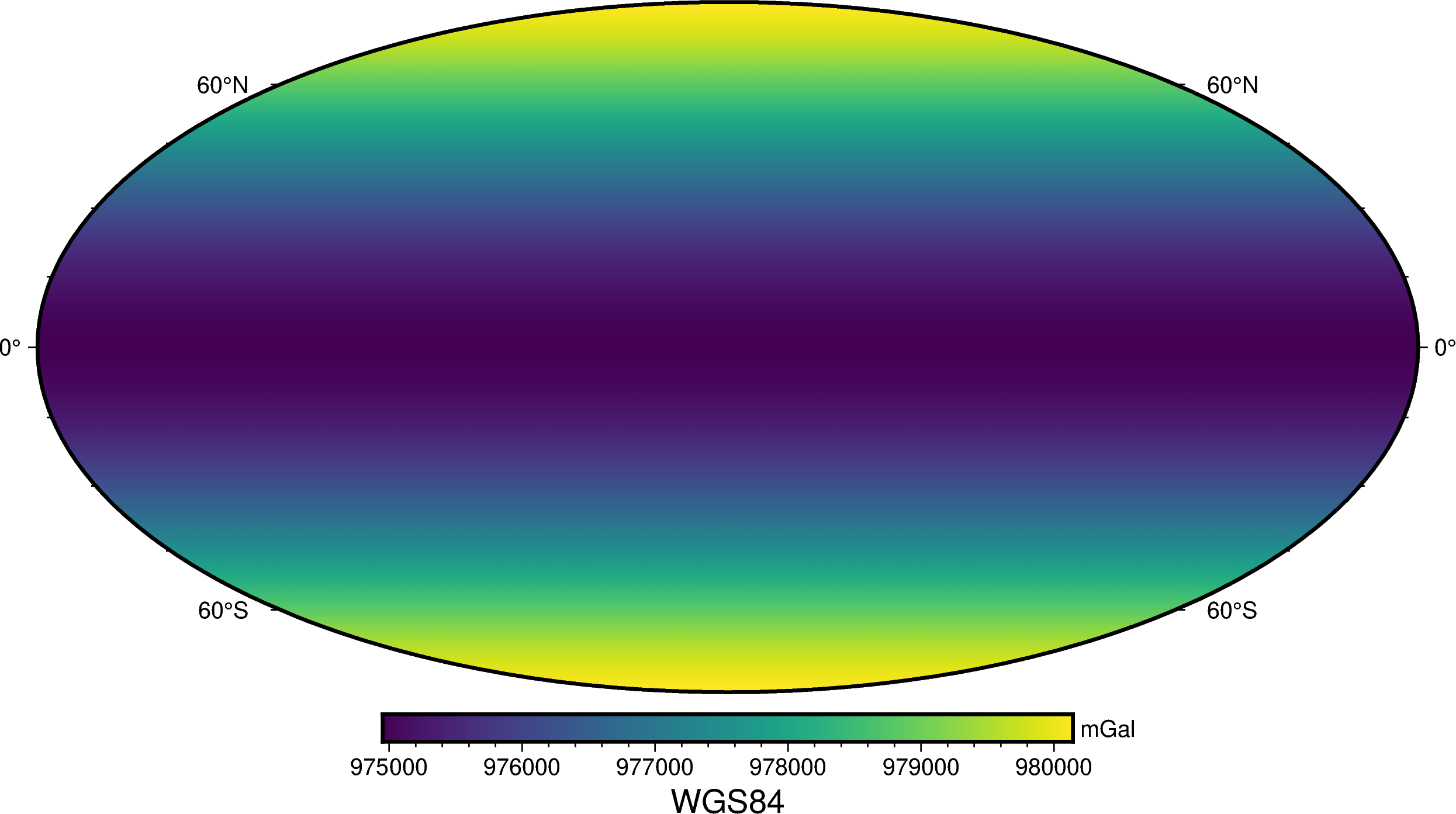
Did you notice?
The calculations were performed at a non-zero height without the need for a
free-air correction. That’s because
method boule.Ellipsoid.normal_gravity implements the closed-form
formula of [Lakshmanan1991] and [LiGotze2001] instead of the classic
Somigliana equation.
This allows us to calculate normal gravity precisely at any height above
the ellipsoid without the need for a free-air correction, which is
particularly useful for geophysics.
These calculations can be performed for any oblate ellipsoid (see Available ellipsoids). Here is the normal gravity of the Martian ellipsoid:
gamma_mars = bl.MARS.normal_gravity(latitude=latitude, height=10_000)
grid_mars = vd.make_xarray_grid(
(longitude, latitude), gamma_mars, data_names="normal_gravity",
)
fig = pygmt.Figure()
fig.grdimage(grid_mars.normal_gravity, projection="W20c", cmap="lajolla")
fig.basemap(frame=["af", "WEsn"])
fig.colorbar(position="JCB+w10c", frame=["af", 'y+l"mGal"', 'x+l"Mars"'])
fig.show()
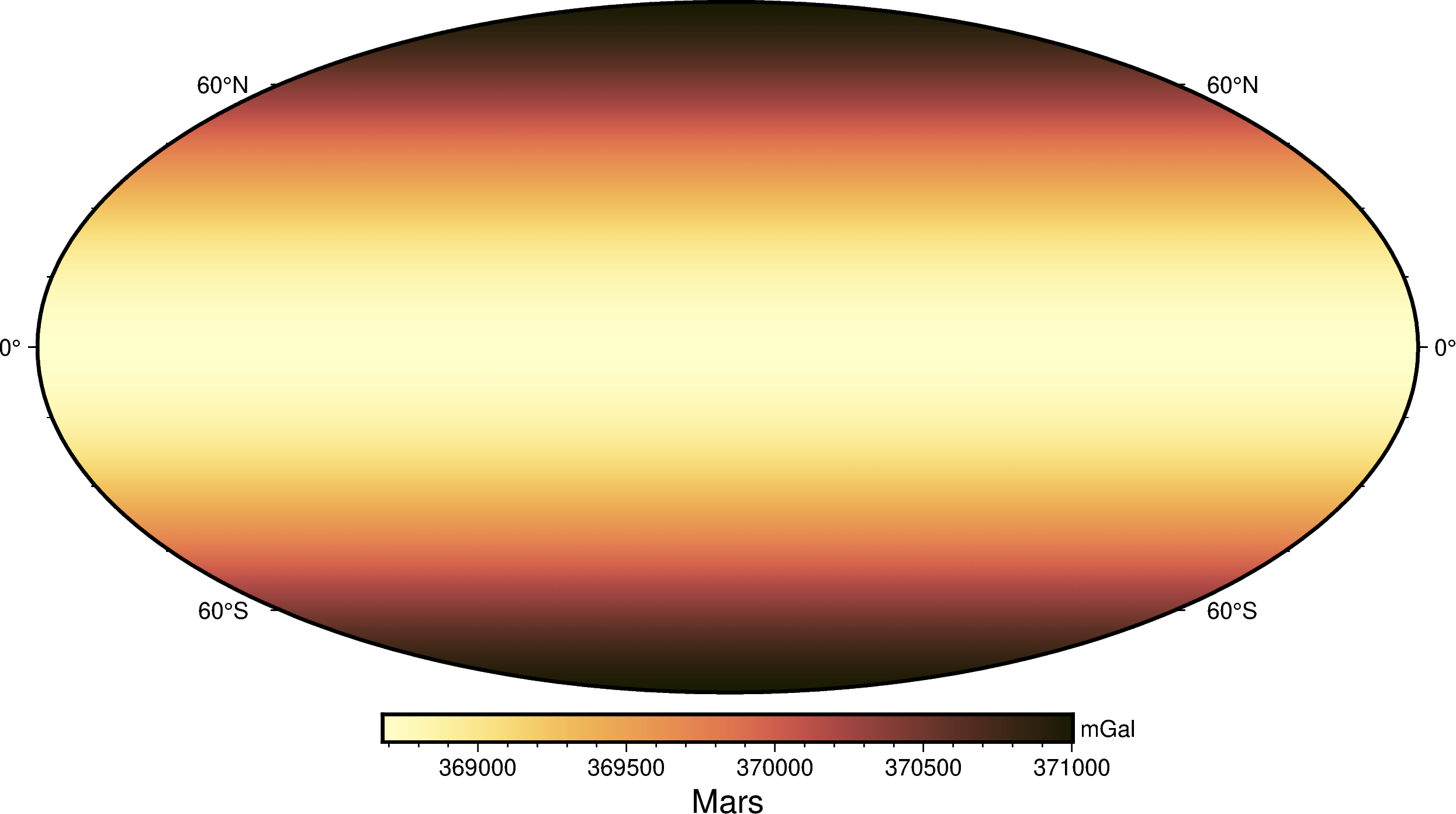
Notice that the overall trend is the same as for the Earth (the Martian ellipsoid is also oblate) but the range of values is different. The mean gravity on Mars is much weaker than on the Earth: around 370,000 mGal or 3.7 m/s² when compared to 970,000 mGal or 9.7 m/s² for the Earth.
Assumptions for oblate ellipsoids
Normal gravity of oblate ellipsoids is calculated under the following assumptions:
The gravity potential is constant on the surface of the ellipsoid.
The internal density structure is unspecified but must lead to a constant potential at the surface.
Important: A homogeneous density ellipsoid does not satisfy the condition of constant potential at the surface. See [Karcol2017] for a thorough discussion.
Spheres#
Method boule.Sphere.normal_gravity performs the normal gravity
calculations for spheres. It behaves mostly the same as the oblate ellipsoid
version except that the latitude is a geocentric spherical latitude instead
of a geodetic latitude (for spheres they are actually the same thing).
gamma = bl.MOON.normal_gravity(latitude=45, height=height)
print(gamma)
[162467.83654908 162447.05499056 162426.27741906 162405.50383356
162384.73423306 162363.96861652 162343.20698292 162322.44933126
162301.69566051 162280.94596965]
This is what the normal gravity of Moon looks like on a map:
gamma = bl.MOON.normal_gravity(latitude=latitude, height=10_000)
grid = vd.make_xarray_grid(
(longitude, latitude), gamma, data_names="normal_gravity",
)
fig = pygmt.Figure()
fig.grdimage(grid.normal_gravity, projection="W20c", cmap="lapaz")
fig.basemap(frame=["af", "WEsn"])
fig.colorbar(position="JCB+w10c", frame=["af", 'y+l"mGal"', 'x+l"Moon"'])
fig.show()
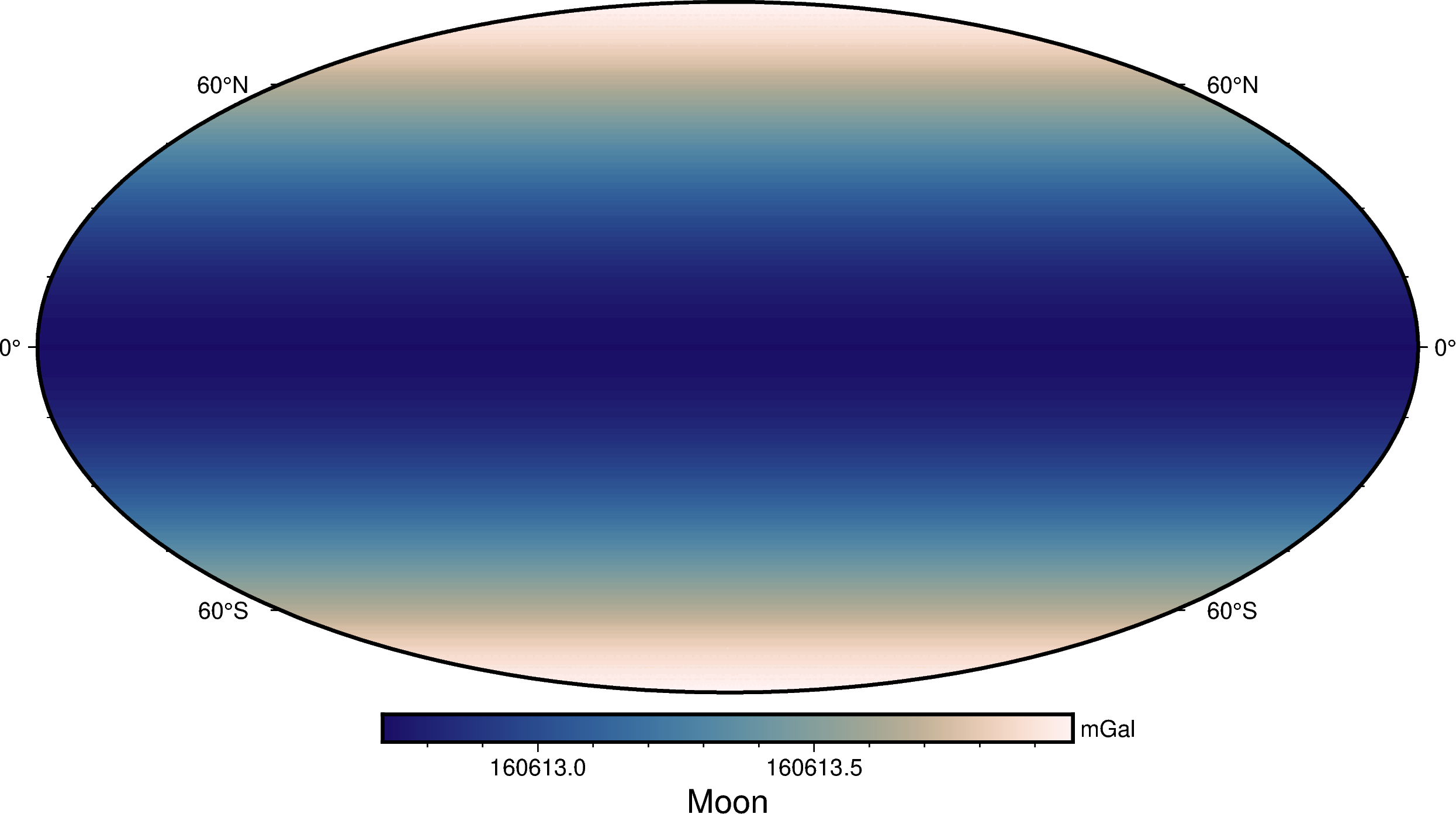
Assumptions for spheres
Normal gravity of spheres is calculated under the following assumptions:
The normal gravity is the magnitude of the gradient of the gravity potential of the sphere.
The internal density structure is unspecified but must be either homogeneous or vary radially (e.g., in concentric layers).
A constant gravity potential on the surface of a rotating sphere is not possible. Therefore, the normal gravity calculated for a sphere is different than that of an oblate ellipsoid (hence why we need a separate method of calculation).
Gravity versus gravitation#
Notice that the variation between poles and equator is much smaller than for the Earth or Mars. That’s because the variation is due solely to the centrifugal acceleration.
We can see this clearly when we calculate the normal gravitation (without
the centrifugal component) using boule.Sphere.normal_gravitation:
gravitation = bl.MOON.normal_gravitation(
height=np.full_like(latitude, 10_000)
)
grid = vd.make_xarray_grid(
(longitude, latitude), gravitation, data_names="normal_gravitation",
)
grid
<xarray.Dataset>
Dimensions: (northing: 361, easting: 721)
Coordinates:
* easting (easting) float64 0.0 0.5 1.0 1.5 ... 359.0 359.5 360.0
* northing (northing) float64 -90.0 -89.5 -89.0 ... 89.0 89.5 90.0
Data variables:
normal_gravitation (northing, easting) float64 1.606e+05 ... 1.606e+05Since there is no centrifugal acceleration, the normal gravitation is due solely to the mass of a sphere and depends only on the height above the sphere and not latitude.
Tip
For spherical bodies it can often be better to use
boule.Sphere.normal_gravitation since services like the
ICGEM offer the ability to generate
grids of observed gravitation (without the centrifugal component).
