Note
Click here to download the full example code
Normal Gravity¶
One of the main uses for ellipsoids in geodesy and geophysics is the computation of normal gravity (usually represented by \(\gamma\)):
Normal gravity is the magnitude of the gradient of the gravity potential (gravitational + centrifugal) generated by the ellipsoid.
The calculation is performed by the boule.Ellipsoid.normal_gravity
method.
It implements the closed-form formula of [LiGotze2001] which can calculate
normal gravity at any latitude and (geometric) height.
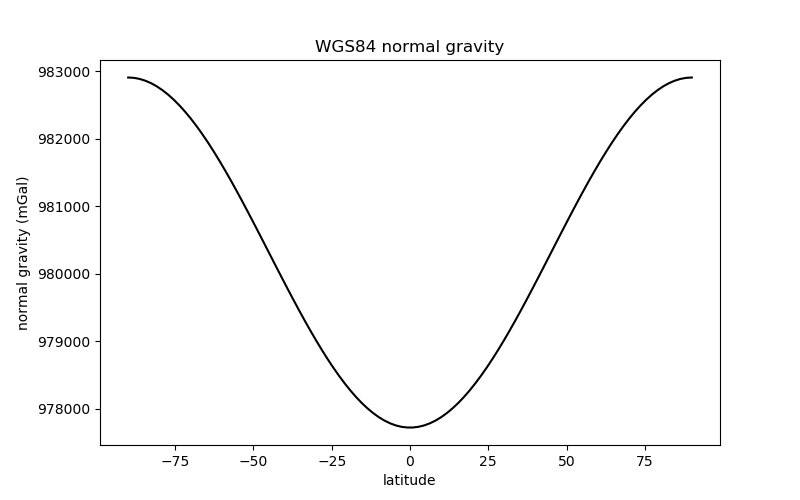
As an example, lets calculate a profile of normal gravity from pole to pole at a height of 1000 m using the WGS84 ellipsoid.
import numpy as np
import matplotlib.pyplot as plt
import boule as bl
latitude = np.linspace(-90, 90, 100)
gamma = bl.WGS84.normal_gravity(latitude, height=1000)
plt.figure(figsize=(8, 5))
plt.plot(latitude, gamma, "-k")
plt.title("WGS84 normal gravity")
plt.xlabel("latitude")
plt.ylabel("normal gravity (mGal)")
plt.show()
This calculation can be performed for any ellipsoid. For example, here is the normal gravity of the Martian ellipsoid:
gamma_mars = bl.MARS.normal_gravity(latitude, height=1000)
plt.figure(figsize=(8, 5))
plt.plot(latitude, gamma_mars, "-k")
plt.title("Mars normal gravity")
plt.xlabel("latitude")
plt.ylabel("normal gravity (mGal)")
plt.show()
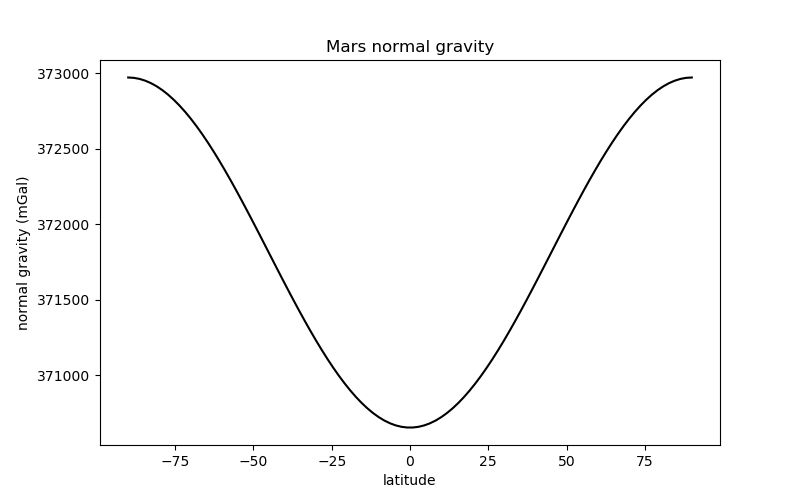
Notice that the overall trend is the same as for the Earth (the Martian ellipsoid is also oblate) but the range of values is different. The mean gravity on Mars is much weaker than on the Earth: around 370,000 mGal or 3.7 m/s² when compared to 970,000 mGal or 9.7 m/s².
Total running time of the script: ( 0 minutes 0.138 seconds)